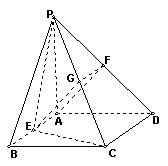
如图，四棱锥P－ABCD的底面是正方形，PA⊥底面ABCD，PA＝2，∠PDA=45°，点E、F分别为棱AB、PD的中点．
（Ⅰ）求证：AF∥平面PCE；
（Ⅱ）求证：平面PCE⊥平面PCD；
（Ⅲ）求三棱锥C－BEP的体积．
如图，四棱锥P－ABCD的底面是正方形，PA⊥底面ABCD，PA＝2，∠PDA=45°，点E、F分别为棱AB、PD的中点．
（Ⅰ）求证：AF∥平面PCE；
（Ⅱ）求证：平面PCE⊥平面PCD；
（Ⅲ）求三棱锥C－BEP的体积．
证明: （Ⅰ）取PC的中点G，连结FG、EG，
∴FG为△CDP的中位线，∴FG
CD，
∵四边形ABCD为矩形，E为AB的中点，
∴ABCD，∴FG
AE，
∴四边形AEGF是平行四边形，∴AF∥EG，
又EG
平面PCE，AF
平面PCE，
∴AF∥平面PCE；
（Ⅱ）∵ PA⊥底面ABCD，
∴PA⊥AD，PA⊥CD，又AD⊥CD，PA
AD=A，
∴CD⊥平面ADP，
又AF平面ADP，∴CD⊥AF，
直角三角形PAD中，∠PDA=45°，∴△PAD为等腰直角三角形，
∴PA＝AD=2， ∵F是PD的中点，∴AF⊥PD，又CDPD=D，∴AF⊥平面PCD，
∵AF∥EG，∴EG⊥平面PCD，
又EG平面PCE， 平面PCE⊥平面PCD；
（Ⅲ）三棱锥C－BEP即为三棱锥P－BCE，
PA是三棱锥P－BCE的高，
Rt△BCE中，BE=1，BC=2，
∴三棱锥C－BEP的体积
V三棱锥C－BEP=V三棱锥P－BCE=
．