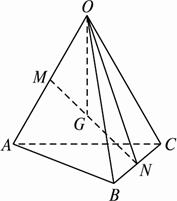
已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC.M、N分别是OA、BC的中
已知空间四边形
OABC中,∠
AOB=∠
BOC=∠
AOC,且
OA=
OB=
OC.
M、
N分别是
OA、
BC的中点,
G是
MN的中点,求证:
OG⊥
BC.
证明:
如图,连结
ON,设∠
AOB=∠
BOC=∠
AOC=
θ,
又设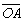
=
a,
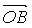
=
b,
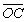
=
c,则|
a|=|
b|=|
c|,
又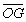
=
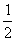
(
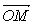
+
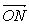
)=
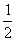
[
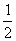
+
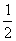
(
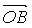
+
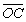
)]
=
(
a+
b+
c),
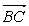
=
c-
b,
∴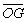
·
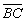
=
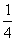
(
a+
b+
c)(
c-
b)
=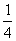
(
a·
c-
a·
b+
b·
c-
b2+
c2-
b·
c)
=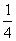
(|
a|
2cos
θ-|
a|
2cos
θ-|
a|
2+|
a|
2)=0.
∴OG⊥BC.

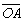
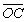 =c,则|a|=|b|=|c|,
=c,则|a|=|b|=|c|,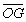
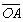 +
+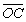 )]
)]![]()
![]()
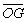
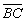 =
=![]()
![]()