已知α=30°,β=60°,γ=300°,OA,OB,OC分别是角α,β,γ的终边.
(1)分别写出两图中阴影部分(含边界)的所有角的集合;
(2)写出图(2)中阴影部分在[0°,360°]上的所有角的集合.
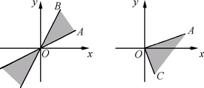
图(1) 图(2)
(例2)
已知α=30°,β=60°,γ=300°,OA,OB,OC分别是角α,β,γ的终边.
(1)分别写出两图中阴影部分(含边界)的所有角的集合;
(2)写出图(2)中阴影部分在[0°,360°]上的所有角的集合.

图(1) 图(2)
(例2)
(1)图(1)中OA可看作α的终边,OB可看作β的终边,故终边落在阴影部分内的角的集合可表示为{θ1|k·180°+30°≤θ1≤k·180°+60°,k∈Z}.
图(2)中OC可看作-60°的终边,故终边落在阴影部分内的角的集合可表示为{θ2|k·360°-60°≤θ2≤k·360°+30°,k∈Z}.
(2)[0°,360°]上所有角的集合为{θ|0°≤θ≤30°或300°≤θ≤360°}.
【精要点评】区域角也称为范围角,表示的是一定范围内角的全体,它是高考的考点之一.表示区域角时要注意考虑问题的范围以及边界的虚实线情况,同时有的学生容易忽视前提,写成[-60°,30°].