如图1,在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a>0)的图像顶
如图1,在平面直角坐标系xOy中,二次函数y=ax
2+bx+c(a>0)的图像顶点为D,与y轴交于点C,与x轴交于点A、B,点A在原点的左侧,点B的坐标为(3,0),OB=OC,tan∠ACO=.
【小题1】求这个二次函数的解析式;
【小题2】若平行于x轴的直线与该抛物线交于点M、N,且以MN为直径的圆与x轴相切,求该圆的半径长度;Com]
【小题3】如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,△AGP的面积最大?求此时点P的坐标和△AGP的最大面积.


【小题1】由OC=OB=3,知C
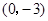
连接AC,在Rt△AOC中,OA=OC×tan∠ACO=
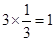
,故A
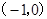
设所求二次函数的表达式为
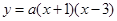
将C
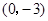
代入得

,解得
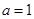
,
∴这个二次函数的表达式为
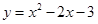
。
【小题1】①当直线MN在x轴上方时,设所求圆的半径为R(R>0),设M在N的左侧,
∵所求圆的圆心在抛物线的对称轴
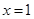
上,
∴N(R+1,R)代入
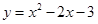
中得
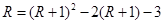
,
解得
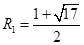
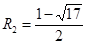
(舍)
②当直线MN在x轴下方时,设所求圆的半径为
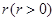
,由①可知N
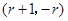
,代入抛物线方程可得
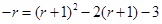
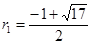
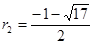
(舍)。
【小题1】

解析:
【小题1】根据已知条件,易求得C、A的坐标,可用待定系数法求出抛物线的解析式;
【小题1】根据抛物线和圆的对称性,知圆心必在抛物线的对称轴上,由于该圆与x轴相切,可用圆的半径表示出M、N的坐标,将其入抛物线的解析式中,即可求出圆的半径;(需注意的是圆心可能在x轴上方,也可能在x轴下方,需要分类讨论)
【小题1】易求得AC的长,由于AC长为定值,当P到直线AG的距离最大时,△APG的面积最大.可过P作y轴的平行线,交AG于Q;设出P点坐标,根据直线AG的解析式可求出Q点坐标,也就求出PQ的长,进而可得出关于△APG的面积与P点坐标的函数关系式,根据函数的性质可求出△APG的最大面积及P点的坐标,根据此时△APG的面积和AG的长,即可求出P到直线AC的最大距离.




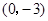
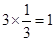 ,故A
,故A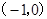
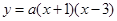
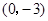 代入得
代入得 ,解得
,解得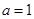 ,
,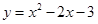 。
。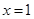 上,
上,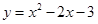 中得
中得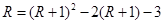 ,
,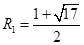
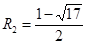 (舍)
(舍)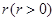 ,由①可知N
,由①可知N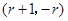 ,代入抛物线方程可得
,代入抛物线方程可得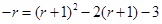
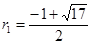
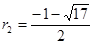 (舍)。
(舍)。 解析:
解析: