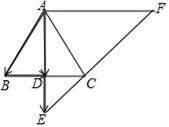
已知：如图，在△ABC中，AB=AC，过点A作AD⊥BC，垂足为点D，延长AD至点E，使DE=
AD，过点A作AF∥BC，交EC的延长线于点F．
（1）设
=
，
=
，用
、的线性组合表示
；
（2）求
的值．
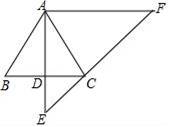
已知：如图，在△ABC中，AB=AC，过点A作AD⊥BC，垂足为点D，延长AD至点E，使DE=AD，过点A作AF∥BC，交EC的延长线于点F．
（1）设=， =，用、的线性组合表示；
（2）求的值．
【考点】*平面向量；等腰三角形的性质．
【分析】（1）由平面向量的三角形法则得到
，然后结合已知条件DE=
AD来求
；
（2）根据平行线截线段成比例和三角形的面积公式进行解答．
【解答】解：（1）∵如图，在△ABC中，AB=AC，AD⊥BC，
∴BD=BC，
∵=，
=
，
∴
=+
=+．
又∵DE=AD，
∴
==
+
，
∴
=
+
=+
++=
+
；
（2）∵DE=AD，AF∥BC，
∴
=
，
=
=
，
∴
=
=•
=
×
=
，
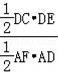
即
=．
