(1)求点A到直线B′C的距离;
(2)求点A到平面BD′的距离;
(3)求点A′到平面AB′D′的距离;
(4)求平面AB′D′与平面BC′D的距离;
(5)求直线AB到平面CDA′B′的距离.
(1)求点A到直线B′C的距离;
(2)求点A到平面BD′的距离;
(3)求点A′到平面AB′D′的距离;
(4)求平面AB′D′与平面BC′D的距离;
(5)求直线AB到平面CDA′B′的距离.
解:
(1)由题意作图,易知点A到直线B′C的距离为正△AB′C的边B′C上的高,其值为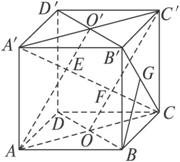
(2)易知直线AO⊥平面BD′,AO的长即为所求,AO=![]() AC=
AC=![]() .
.
(3)易知平面A′ACC′⊥平面AB′D′,在矩形A′ACC′中,易知A′C⊥O′A,设A′C∩O′A=E,且A′E=![]() A′C=
A′C=![]() ,
,
所以A′E为点A′到平面AB′D′的距离.
(4)易知A′C⊥平面AB′D′,A′C⊥平面BC′D,设直线A′C分别交平面AB′D′、平面BC′D于点E、F,则EF的长为平面AB′D′与平面BC′D的距离,
于是EF=![]() A′C=
A′C=![]() .
.
(5)因为直线AB∥平面CDA′B′,所以所求的距离即为点B到平面CDA′B′的距离BG(由BG⊥直线B′C,直线BG⊥平面A′B′CD知),此距离为![]() BC′=
BC′=![]() .
.
点拨:
求解空间距离,最基本的方法是直接法,做选择,填空题时,往往比向量法简单.