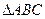 和
和 摆放在一起,
摆放在一起, 为公共顶点,
为公共顶点,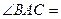
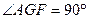 ,它们的斜边长为2,若
,它们的斜边长为2,若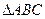 固定不动,
固定不动, 绕点
绕点 旋转,
旋转, 、
、 与边
与边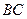 的交点分别为
的交点分别为 、
、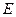 (点
(点 不与点
不与点 重合,点
重合,点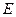 不与点
不与点 重合),设
重合),设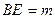 ,
,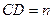 .
.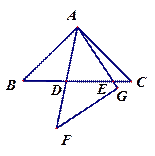
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对加以证明.
(2)求
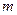 与
与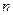 的函数关系式,直接写出自变量
的函数关系式,直接写出自变量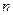 的取值范围.
的取值范围. 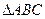 和
和 摆放在一起,
摆放在一起, 为公共顶点,
为公共顶点,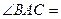
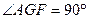 ,它们的斜边长为2,若
,它们的斜边长为2,若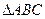 固定不动,
固定不动, 绕点
绕点 旋转,
旋转, 、
、 与边
与边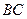 的交点分别为
的交点分别为 、
、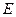 (点
(点 不与点
不与点 重合,点
重合,点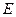 不与点
不与点 重合),设
重合),设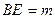 ,
,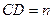 .
.
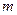 与
与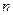 的函数关系式,直接写出自变量
的函数关系式,直接写出自变量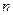 的取值范围.
的取值范围.  ,或
,或 (
( )解析:
)解析: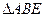 ∽
∽ ,
, ∽
∽ .
.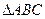 和
和 是全等的等腰直角三角形,且
是全等的等腰直角三角形,且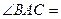
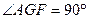 ,
, 
 , 又∵
, 又∵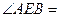
 (公共角),
(公共角),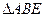 ∽
∽ . 同理可证
. 同理可证 ∽
∽ .
.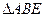 ∽
∽ ,
, ∽
∽ ,则有
,则有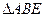 ∽
∽ .
.
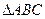 是等腰直角三角形,且
是等腰直角三角形,且 ,
, ,又
,又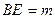 ,
,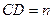 ,
,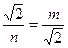 ,即
,即 ,或
,或 (
( )
)