иӢҘжӨӯеңҶ![]() зҡ„ж–№зЁӢдёә
зҡ„ж–№зЁӢдёә![]() пјҢ
пјҢ![]() гҖҒ
гҖҒ![]() жҳҜе®ғзҡ„е·ҰгҖҒеҸіз„ҰзӮ№пјҢжӨӯеңҶ
жҳҜе®ғзҡ„е·ҰгҖҒеҸіз„ҰзӮ№пјҢжӨӯеңҶ![]() иҝҮзӮ№
иҝҮзӮ№![]() пјҢдё”зҰ»еҝғзҺҮдёә
пјҢдё”зҰ»еҝғзҺҮдёә![]() пјҺ
пјҺ
пјҲв… пјүжұӮжӨӯеңҶзҡ„ж–№зЁӢпјӣ
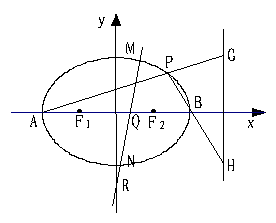
пјҲв…Ўпјүи®ҫжӨӯеңҶзҡ„е·ҰеҸійЎ¶зӮ№дёә![]() гҖҒ
гҖҒ![]() пјҢзӣҙзәҝ
пјҢзӣҙзәҝ![]() зҡ„ж–№зЁӢдёә
зҡ„ж–№зЁӢдёә![]() пјҢ
пјҢ![]() жҳҜжӨӯеңҶдёҠд»»дёҖзӮ№пјҢзӣҙзәҝ
жҳҜжӨӯеңҶдёҠд»»дёҖзӮ№пјҢзӣҙзәҝ![]() гҖҒ
гҖҒ![]() еҲҶеҲ«дәӨзӣҙзәҝ
еҲҶеҲ«дәӨзӣҙзәҝ![]() дәҺ
дәҺ![]() гҖҒ
гҖҒ![]() дёӨзӮ№пјҢжұӮ
дёӨзӮ№пјҢжұӮ![]() зҡ„еҖјпјӣ
зҡ„еҖјпјӣ
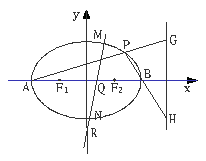
пјҲв…ўпјүиҝҮзӮ№![]() д»»ж„ҸдҪңзӣҙзәҝ
д»»ж„ҸдҪңзӣҙзәҝ![]() пјҲдёҺ
пјҲдёҺ![]() иҪҙдёҚеһӮзӣҙпјүдёҺжӨӯеңҶ
иҪҙдёҚеһӮзӣҙпјүдёҺжӨӯеңҶ![]() дәӨдәҺ
дәӨдәҺ![]() гҖҒ
гҖҒ![]() дёӨзӮ№пјҢдёҺ
дёӨзӮ№пјҢдёҺ![]() иҪҙдәӨдәҺ
иҪҙдәӨдәҺ![]() зӮ№
зӮ№![]() пјҢ
пјҢ![]() пјҺиҜҒжҳҺпјҡ
пјҺиҜҒжҳҺпјҡ ![]() дёәе®ҡеҖјпјҺ
дёәе®ҡеҖјпјҺ