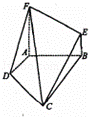
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.
(Ⅰ)证明:在平面EBC上,一定存在过C的直线l与直线FD平行;
(Ⅱ)求二面角F﹣CD﹣A的余弦值.
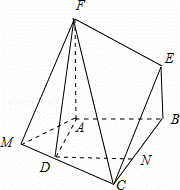
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.
(Ⅰ)证明:在平面EBC上,一定存在过C的直线l与直线FD平行;
(Ⅱ)求二面角F﹣CD﹣A的余弦值.

考点:
二面角的平面角及求法;直线与平面平行的判定.
专题:
空间角.
分析:
(Ⅰ)利用线面、面面平行的判定和性质定理即可证明;
(Ⅱ)利用相似三角形的性质、三垂线定理、线面角的定义即可得出.
解答:
(Ⅰ)证明:由已知得,BE∥AF,BC∥AD,BE∩BC=B,AD∩AF=A,
∴平面BCE∥平面ADF.
设平面DFC∩平面BCE=l,则l过C点.
∵平面BCE∥平面ADF,平面DFC∩平面BCE=l,平面DFC∩平面ADF=DF.
∴DF∥l.证毕
(Ⅱ)解:∵FA⊥AB,FA⊥CD,AB与CD相交,
∴FA⊥平面ABCD.
过点A作AM⊥CD,垂足为M,连接FM,根据三垂线定理可得FM⊥CM,∴∠FMA是二面角F﹣CD﹣A的平面角.
过D点作DN⊥BC交BC于点N,则四边形ABND是矩形,∴DN=2,CN=1,∴CD=![]() .
.
∵△AMD∽△DNC,∴![]() ,∴
,∴![]() =
=![]() .
.
在Rt△AMF中,由勾股定理可得![]() =
=![]() ,
,
∴cos∠AMF=![]() =
=![]() .
.
∴二面角F﹣CD﹣A的余弦值是![]() .
.
点评:
熟练掌握线面、面面平行的判定和性质定理、相似三角形的性质、三垂线定理、线面角的定义是解题的关键.