已知数列{an}的前n项和为Sn，且满足：a1＝a(a≠0)，an＋1＝rSn(n∈N*，r

已知数列{a_n}的前n项和为S_n，且满足：a₁＝a(a≠0)，a_n＋1＝rS_n(n∈N^*，r∈R，r≠－1)．

(1)求数列{a_n}的通项公式；

(2)若存在k∈N^*，使得S_k＋1，S_k，S_k＋2成等差数列，试判断：对于任意的m∈N^*，且m≥2，a_m＋1，a_m，a_m＋2是否成等差数列，并证明你的结论．

解析　(1)由已知a_n＋1＝rS_n，可得a_n＋2＝rS_n＋1，两式相减可得a_n＋2－a_n＋1＝r(S_n＋1－S_n)＝ra_n＋1，即a_n＋2＝(r＋1)a_n＋1，又a₂＝ra₁＝ra，

所以当r＝0时，数列{a_n}为：a,0，…，0，…；

当r≠0，r≠－1时，由已知a≠0，所以a_n≠0(n∈N^*)，

于是由a_n＋2＝(r＋1)a_n＋1，可得＝r＋1(n∈N^*)，

∴a₂，a₃，…，a_n，…成等比数列，

∴当n≥2时，a_n＝r(r＋1)^n－2a.

综上，数列{a_n}的通项公式为a_n＝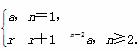

(2)对于任意的m∈N^*，且m≥2，a_m＋1，a_m，a_m＋2成等差数列．证明如下：

当r＝0时，由(1)知，a_n＝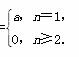

∴对于任意的m∈N^*，且m≥2，a_m＋1，a_m，a_m＋2成等差数列．

当r≠0，r≠－1时，∵S_k＋2＝S_k＋a_k＋1＋a_k＋2，S_k＋1＝S_k＋a_k＋1.若存在k∈N^*，

使得S_k＋1，S_k，S_k＋2成等差数列，则S_k＋1＋S_k＋2＝2S_k，

∴2S_k＋2a_k＋1＋a_k＋2＝2S_k，即a_k＋2＝－2a_k＋1.

由(1)知，a₂，a₃，…，a_m，…的公比r＋1＝－2，于是

对于任意的m∈N^*，且m≥2，a_m＋1＝－2a_m，从而a_m＋2＝4a_m，

∴a_m＋1＋a_m＋2＝2a_m，即a_m＋1，a_m，a_m＋2成等差数列．

综上，对于任意的m∈N^*，且m≥2，a_m＋1，a_m，a_m＋2成等差数列．