е·ІзҹҘfпјҲ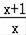
 пјү=
пјү=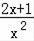
 пјҢеҲҷпјҲгҖҖгҖҖпјүВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҢеҲҷпјҲгҖҖгҖҖпјүВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
AпјҺfпјҲxпјү=x2+1пјҲxвү 0пјүВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В BпјҺfпјҲxпјү=x2+1пјҲxвү 1пјүВ В В CпјҺfпјҲxпјү=x2п№Ј1пјҲxвү 1пјүВ В В DпјҺfпјҲxпјү=x2п№Ј1пјҲxвү 0пјү
CгҖҗиҖғзӮ№гҖ‘еҮҪж•°и§ЈжһҗејҸзҡ„жұӮи§ЈеҸҠеёёз”Ёж–№жі•пјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
гҖҗдё“йўҳгҖ‘иҪ¬еҢ–жҖқжғіпјӣжҚўе…ғжі•пјӣеҮҪж•°зҡ„жҖ§иҙЁеҸҠеә”з”ЁпјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
гҖҗеҲҶжһҗгҖ‘з”ұfпјҲ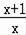
 пјү=
пјү=
 пјҢеҸҳеҪўдёә
пјҢеҸҳеҪўдёә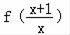
 =
=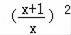
 п№Ј1пјҢеҚіеҸҜеҫ—еҮәпјҺВ В В В В В В В В В В В В В В В В В
п№Ј1пјҢеҚіеҸҜеҫ—еҮәпјҺВ В В В В В В В В В В В В В В В В В
гҖҗи§Јзӯ”гҖ‘и§Јпјҡз”ұ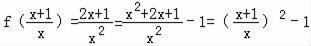
 пјҢВ В В В В В В В В В В В
пјҢВ В В В В В В В В В В В
еҫ—fпјҲxпјү=x2п№Ј1пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
еҸҲвҲө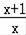
 вү 1пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вү 1пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙfпјҲxпјү=x2п№Ј1зҡ„xвү 1пјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
ж•…йҖүпјҡCпјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
гҖҗзӮ№иҜ„гҖ‘жң¬йўҳиҖғжҹҘдәҶеҮҪж•°зҡ„и§ЈжһҗејҸжұӮжі•пјҢиҖғжҹҘдәҶжҺЁзҗҶиғҪеҠӣдёҺи®Ўз®—иғҪеҠӣпјҢеұһдәҺеҹәзЎҖйўҳпјҺВ В В В В В В В В В В В В В В В В
![]()
![]() пјү=
пјү=![]()
![]() пјҢеҲҷпјҲгҖҖгҖҖпјүВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҢеҲҷпјҲгҖҖгҖҖпјүВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В 