(理)已知数列{an}的前n项和为Sn,且满足a1=,an+2SnSn-1=0(n≥2),(1)判断{}是否

(1)判断{}是否为等差数列?并证明你的结论;

(2)求S_n和a_n;

(3)求证:S₁²+S₂²+…+S_n²≤.

(文)数列{a_n}的前n项和S_n(n∈N

(1)求证:数列{a_n+3}是等比数列;

(2)求数列{a_n}的通项公式;

(3)数列{a_n}中是否存在成等差数列的三项?若存在,求出一组适合条件的三项;若不存在,说明理由.

(理)(1)解

当n≥2时,a_n=S_n-S_n-1,即S_n-S_n-1=-2S_nS_n-1,                                        

∴=2.

故{}是以2为首项,以2为公差的等差数列.                                  

(2)解

当n≥2时,a_n=-2S_nS_n-1=;                                           

当n=1时,a₁=.

∴a_n=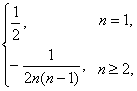                                                 

(3)证法一

②假设n=k时,不等式成立,即≤成立.

则当n=k+1时,

≤

=

=

＜

=,

即当n=k+1时,不等式成立.

由①②可知对任意n∈N

证法二

=

=

≤

=

=.

(文)(1)证明

∴a_n+1=S_n+1-S_n=2a_n+1-3(n+1)-2a_n+3n.

∴a_n+1=2a_n+3.                                                               

∴a_n+1+3=2(a_n+3).

∴=2.

又a₁=S₁=2a₁-3,a₁=3,

∴a₁+3=6.                                                                 

∴数列{a_n+3}成以6为首项以2为公比的等比数列.                             

(2)解

∴a_n=3·2ⁿ-3.                                                                 

(3)解

∴2a_p=a_s+a_r.

∴2(3·2^p-3)=3·2^s-3+3·2^r-3.

∴2^p+1=2^s+2^r,                                                               

即2^p-s+1=1+2^r-s.                                                               (*)

∵s、p、r∈N

∴2^p-s+1为偶数,1+2^r-s为奇数.

∴(*)为矛盾等式,不成立.

故这样的三项不存在.