(本小题满分12分)
妯图,在直三棱柱![]() 中,平面
中,平面![]() 丄侧面
丄侧面![]()
(I )求证:AB丄BC
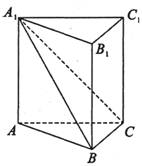 (II)若直线AC与平面
(II)若直线AC与平面![]() 所成的角为
所成的角为![]() ,二面角的大小为
,二面角的大小为![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并予以证明.
的大小关系,并予以证明.
(本小题满分12分)
妯图,在直三棱柱![]() 中,平面
中,平面![]() 丄侧面
丄侧面![]()
(I )求证:AB丄BC
 (II)若直线AC与平面
(II)若直线AC与平面![]() 所成的角为
所成的角为![]() ,二面角的大小为
,二面角的大小为![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并予以证明.
的大小关系,并予以证明.
【解及证】(Ⅰ)证明:如右图,过点A在平面A1ABB1内作AD⊥A1B于D,…………1分
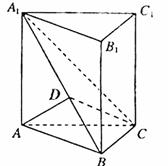 则由平面A1BC⊥侧面A1ABB1于A1B,得AD⊥平面A1BC, …………2分
则由平面A1BC⊥侧面A1ABB1于A1B,得AD⊥平面A1BC, …………2分
又BC![]() 平面A1BC,∴AD⊥BC. …………3分
平面A1BC,∴AD⊥BC. …………3分
∵三棱柱ABC—A1B1C1是直三棱柱,则AA1⊥底面ABC,∴AA1⊥BC. …4分
又AA1∩AD=A,从而BC⊥侧面A1ABB1, …………5分
又AB![]() 侧面A1ABB1,故AB⊥BC ………………………6分
侧面A1ABB1,故AB⊥BC ………………………6分
(Ⅱ)解法1:连接CD,则由(Ⅰ)知![]() 是直线AC与平面A1BC所成的角,…………7分
是直线AC与平面A1BC所成的角,…………7分
![]() 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即![]() ………..…8分
………..…8分
于是在Rt△ADC中,![]() ………9分 在Rt△ADB中,
………9分 在Rt△ADB中,![]() ……….10分
……….10分
 由AB<AC,得
由AB<AC,得![]() 又
又![]() 所以
所以![]() …………………….12分
…………………….12分
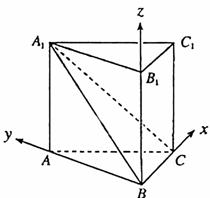
解法2:由(Ⅰ)知,以点B为坐标原点,以BC、BA、BB1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系, ………………7分
设AA1=a,AC=b,AB=c,则 B(0,0,0), A(0,c,0),
![]() 于是
于是
![]() ,
,![]() ,
,![]()
![]() ……8分
……8分
设平面A1BC的一个法向量为![]() =(x,y,z),则由
=(x,y,z),则由 得
得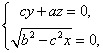 ……9分
……9分
可取![]() =(0,
=(0,![]() ,c),于是
,c),于是![]()
![]()
![]() c>0,
c>0,![]() 与n的夹角
与n的夹角![]() 为锐角,则
为锐角,则![]() 与
与![]() 互为余角.
互为余角.
∴sinθ=cosβ= =
=![]() , cosφ=
, cosφ= ,
,
∴![]() 于是由
于是由![]() <b,得
<b,得![]() 即
即![]() 又
又![]()
∴![]() …..12分.
…..12分.