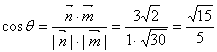三棱锥P―ABC，截面A1B1C1//底面ABC，∠BAC=90°，PA⊥底面ABC，A1A=
（1）求证：平面A1AD⊥平面BCC1B1；
（2）求二面角A―CC1―B的大小。
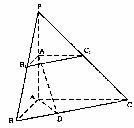
三棱锥P―ABC，截面A1B1C1//底面ABC，∠BAC=90°，PA⊥底面ABC，A1A=
（1）求证：平面A1AD⊥平面BCC1B1；
（2）求二面角A―CC1―B的大小。
解：（1）
，
A到BC距离
令d=AD′，BD′=
又BD=
与D重合
（2）建系：A（0，0，0），AB为x轴，AC为y轴，AP为z轴，
则B（
，0，0），C（0，2，0），A1（0，0，
），C（0，1，）
平面ACC1的法向量
（1，0，0）
在平面BCC1内，
设法向量为
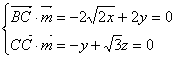
令
