已知椭圆C： +=1（a＞b＞0）的长轴长为2，右焦点F（1，0），过F作两

已知椭圆C： +=1（a＞b＞0）的长轴长为2，右焦点F（1，0），过F作两条互相垂直的直线分别交椭圆G于点A，B和C，D，设AB，CD的中点分别为P，Q．

（Ⅰ）求椭圆G的方程；

（Ⅱ）若直线AB，CD的斜率均存在，求•的最大值，并证明直线PQ与x轴交于定点．

【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．

【分析】（Ⅰ）由椭圆的长轴长为2，右焦点F（1，0），列出方程组求出a，b，由此能求出椭圆G的方程．

（Ⅱ）F（1，0），由题意设直线AB的方程为y=k（x﹣1），k≠0，由，得（3k²+2）x²﹣6k²x+3k²﹣6=0，由此利用韦达定理、中点坐标公式分别求出AB的中点P，CD的中点Q，从而求出k=±1时，有最大值．当k=±1时，直线PQ的方程为x=，恒过定点（，0），当直线有斜率时，求出直线PQ的方程，由此能求出直线PQ恒过定点（）．

【解答】解：（Ⅰ）∵椭圆C： +=1（a＞b＞0）的长轴长为2，右焦点F（1，0），

∴，解得a=，b=，

∴椭圆G的方程为=1．

（Ⅱ）F（1，0），由题意设直线AB的方程为y=k（x﹣1），k≠0，

由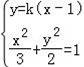，得（3k²+2）x²﹣6k²x+3k²﹣6=0，

设A（x₁，y₁），B（x₂，y₂），则，y₁+y₂=k（x₁+x₂）﹣2k=，

∴AB的中点P（，），

又由题意得直线CD的方程为y=﹣，

同理，得CD的中点Q（），

∴==

=≤=，

当且仅当，即k=±1时，有最大值．

又当直线PQ⊥x轴时， =，

即k=±1时，直线PQ的方程为x=，恒过定点（，0），

当直线有斜率时，k_PQ==，

∴直线PQ的方程为y﹣，

令y=0，得x===，恒过定点（），

综上，直线PQ恒过定点（）．