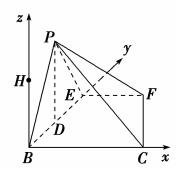
.如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上.过点
上.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置(点
的位置(点![]() 与
与![]() 重合),使得
重合),使得![]() .
.
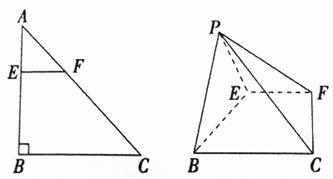
(Ⅰ)求证:![]() .
.
(Ⅱ)试问:当点![]() 在线段
在线段![]() 上移动时,二面角
上移动时,二面角![]() 的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
.如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上.过点
上.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置(点
的位置(点![]() 与
与![]() 重合),使得
重合),使得![]() .
.

(Ⅰ)求证:![]() .
.
(Ⅱ)试问:当点![]() 在线段
在线段![]() 上移动时,二面角
上移动时,二面角![]() 的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
证明:(Ⅰ)在![]() 中,
中,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(Ⅱ)在平面![]() 内,过点
内,过点![]() 作
作![]() 于点
于点![]() ,
,
由(Ⅰ)知![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
在平面![]() 内过点
内过点![]() 作直线
作直线![]() ,则
,则![]() 平面
平面![]() .
.
如图所示,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
设![]() ,
,
又因为![]() ,
,
所以![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
, .
.
从而![]() ,
,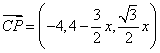 .
.
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以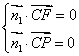 ,即
,即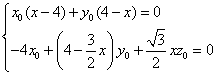 ,
,
所以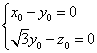 ,
,
取![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]()
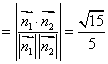 .
.
因此当点![]() 在线段
在线段![]() 上移动时,二面角
上移动时,二面角![]() 的平面角的余弦值为定值,且定值为
的平面角的余弦值为定值,且定值为![]() .
.