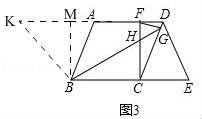
已知，平行四边形ABCD，E在BC延长线上，连接DE，∠A+∠E=180°．
（1）如图1，求证：CD=DE；
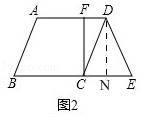
（2）如图2，过点C作BE的垂线，交AD于点F，求证：BE=AF+3DF；
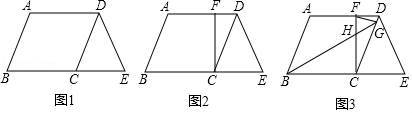
（3）如图3，在（2）的条件下，∠ABC的平分线，交CD于G，交CF于H，连接FG，若∠FGH=45°，DF
=8，CH=9，求BE的长．
已知，平行四边形ABCD，E在BC延长线上，连接DE，∠A+∠E=180°．
（1）如图1，求证：CD=DE；
（2）如图2，过点C作BE的垂线，交AD于点F，求证：BE=AF+3DF；
（3）如图3，在（2）的条件下，∠ABC的平分线，交CD于G，交CF于H，连接FG，若∠FGH=45°，DF=8，CH=9，求BE的长．
【解答】解：（1）∵四边形ABCD是平行四边形，
∴∠A=∠BCD，
∵∠A+∠E=180°，∠BCD+∠DCE=180°，
∴∠DCE=∠E，
∴CD=DE；
（2）如图2，过点D作DN⊥BE于N，
∵CF⊥BE，
∴∠DNC=∠BCF=90°，
∴FC∥DN，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴四边形CFDN是矩形，
∴FD=CN，
∵CD=DE，DN⊥CE，
∴CN=NE=FD，
∵四边形ABCD是平行四边形，
∴BC=AD=AF+FD，
∴BE=AF+3DF．
（3）如图3，过点B作BM⊥AD于点M，延长FM至K，使KM=HC．连接BK，
∵□ABCD，
∴AB∥CD，
∴∠ABG=∠BGC，
∵BG平分∠ABC，
∴设∠ABG=∠CBG=∠BGC=α，
∴BC=CG，
∵∠FGH=45°，
∴∠FGC=45°+α，
∵∠BCF=90°，
∴∠BHC=∠FHG=90°﹣α，
∴∠HFG=45°+α=∠FGC，
∴FC=CG=BC，
∵BM⊥AD，
∴∠MBC=90°=∠FCE=∠MFC，
∴四边形BCFM是矩形，
∵BC=FC，
∴四边形BCFM是正方形，
∴BM=MF=BC=AD，
∴MA=DF=8，
∵∠KMB=∠BCH=90°，KM=CH，
∴△BMK≌△BCH，
∴KM=CH=9，∠KBM=∠CBH=α，∠K=∠BHC=90°﹣α，
∵∠MBC=90°，
∴∠MBA=90°﹣2α，
∴∠KBA=90°﹣α=∠K，
∴AB=AK=8+9=17，
在Rt△ABM中，∠BMA=90°，BM=
=15，
∴AD=BC=BM=15，[来源:学&科&网]
∴AF=AD﹣DF=15﹣8=7，
∴BE=AF+3DF=7+3×8=31．
