在△ABC中，AB=AC，∠BAC=
（
），将线段BC绕点B逆时针旋转60°得到线段BD。
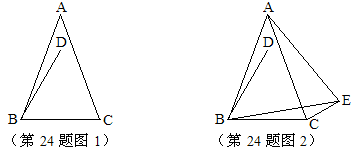
（1）如图1，直接写出∠ABD的大小（用含的式子表示）；
（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
（3）在（2）的条件下，连结DE，若∠DEC=45°，求的值。
在△ABC中，AB=AC，∠BAC=（），将线段BC绕点B逆时针旋转60°得到线段BD。
（1）如图1，直接写出∠ABD的大小（用含的式子表示）；
（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
（3）在（2）的条件下，连结DE，若∠DEC=45°，求的值。
解析：【解析】（1）
（2）
为等边三角形
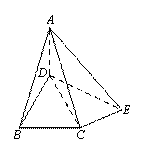
证明连接
、
、
∵线段
绕点
逆时针旋转
得到线段
则
，
又∵
∴
且
为等边三角形.
在
与
中
∴≌
（SSS）
∴
∵
∴
在与
中
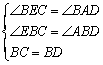
∴≌（AAS）
∴
∴为等边三角形
（3）∵
，
∴
又∵
∴
为等腰直角三角形
∴
∵
∴
而
∴
【点评】本题是初中数学重要模型“手拉手”模型的应用，从本题可以看出积累掌握常见模
型、常用辅助线对于平面几何的学习是非常有帮助的.