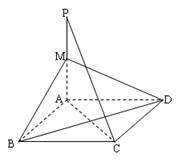
如图，四边形ABCD是菱形，PA⊥平面ABCD，M为PA的中点.
（Ⅰ）求证：PC∥平面BDM；
（Ⅱ）若PA＝AC＝
，BD＝
，求直线BM与平面PAC所成的角.
如图，四边形ABCD是菱形，PA⊥平面ABCD，M为PA的中点.
（Ⅰ）求证：PC∥平面BDM；
（Ⅱ）若PA＝AC＝，BD＝，求直线BM与平面PAC所成的角.
（Ⅰ）证明略（Ⅱ）60°
（Ⅰ）设AC与BD的交点为O，连结OM.因为ABCD是菱形，则O为AC中点.
又M为PA的中点，所以OM∥PC. （3分）
因为OM在平面BDM内，所以PC∥平面BDM. （4分）
（Ⅱ）因为ABCD是菱形，则BD⊥AC.
又PA⊥平面ABCD，则PA⊥BD.
所以BD⊥平面PAC.
所以∠BMO是直线BM与平面PAC所成的角. （7分）
因为PA⊥平面ABCD，所以PA⊥AC. 在Rt△PAC中，因为PA＝AC＝
，则PC＝2.
又点M与点O分别是PA与AC的中点，则MO＝
PC＝1. （9分）
又BO＝BD＝
，在Rt△BOM中，tan∠BMO＝
，所以∠BMO＝60°.
故直线BM与平面PAC所成的角是60°. （12分）