(09年湖北重点中学联考理)(12分)
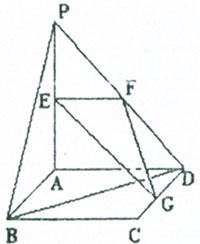
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=900,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
(1)求证:PB∥平面EFG;
(2)求异面直线EG与BD所成的角;
(09年湖北重点中学联考理)(12分)
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=900,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
(1)求证:PB∥平面EFG;
(2)求异面直线EG与BD所成的角;

解析: 解法一:(1)证明:取AB中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH//AD//EF,
∴E,F,G,H四点共面。又H为AB中点,
∴EH//PB。又![]() 面EFG,
面EFG,![]() 平面EFG,
平面EFG,
∴PB//面EFG。

(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角。在Rt△MAE中,![]() ,
,
同理![]() ,又
,又![]() ,
,
∴在Rt△MGE中,![]()
故异面直线EG与BD所成的角为![]() 。
。 ![]() 12分
12分
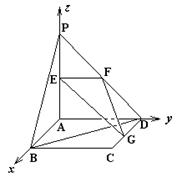
解法二:(1)建立如图所示的空间直角坐标系A-xyz,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 。(1)证明:∵
。(1)证明:∵![]() ,
,![]() ,
,![]() ,设
,设![]() ,即
,即![]()
解得![]() 。∴
。∴![]() ,又∵
,又∵![]() 与
与![]() 不共线,∴
不共线,∴![]() 、
、![]() 与
与![]() 共面。∵
共面。∵![]() 平面EFG,∴PB//平面EFG。
平面EFG,∴PB//平面EFG。![]() 6分
6分
(2)解:∵![]() ,
,![]() ,∴
,∴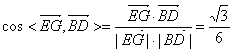 。
。