已知:如图,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.

⑴ 求证:BC=CD.
⑵ 若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变,猜想:BC边和邻边CD的长度是否一定相等?请证明你的结论.
⑶ 探究:在⑵的情况下,如果再限制∠BAD=60°,那么相邻两边AB、AD和对角线AC之间有什么确定的数量关系?需说明理由.
⑴见解析⑵ 一定相等,见解析⑶AB+AD=
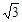
AC,理由见解析解析:
解:⑴ 证明:∵AC平分∠BAD,
∴∠BAC=∠DAC.
又∵∠D =∠B=Rt∠,AC公用,
∴△ABC≌△ADC.
∴ BC=CD. …………………………………………2分
⑵ 一定相等 . ………………………………………………3分
证明:如图2,不妨设∠B为锐角,作CE⊥AB于E,则点E必在线段AB上
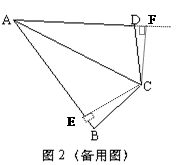
∵∠B和∠D互为补角,
∴∠D是钝角,作CF⊥AD于F,
则点F必在线段AD的延长线上.
∴∠CDF与∠ADC互补.
∴∠B=∠CDF.
又∵AC是∠BAD的平分线, ∴ CE=CF.
∴Rt△BCE≌Rt△DCF
∴ BC=CD. ………………………………………………6分
⑶ AB+AD=
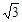
AC. ………………………………………………7分
理由是:图2中,由已知条件,易知AE=AF,BE=DF.
∴AB+AD=(AE+BE)+(AF-DF)=AE+AF=2AE.
当∠BAD=60°时,∠CAE=30°,AE=
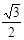
AC.
∴AB+AD=2AE=
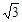
AC. ………………………………………………10分
(1)由AC平分∠BAD与∠B和∠D都是直角,以及AC是公共边,根据AAS即可证得△ABC≌△ADC,则可得BC=CD;
(2)首先不妨设∠B为锐角,作CE⊥AB于E,则点E必在线段AB上,由∠B和∠D互为补角,可得∠D是钝角,作CF⊥AD于F,则点F必在线段AD的延长线上,则可得∠D=∠CBF,又由AC是∠BAD的平分线,与CE=CF,即可证得Rt△BCF≌Rt△DCE,则可得BC=CD;
(3)在图2中,由已知条件,易知AE=AF,BE=DF,则可得AB+AD=(AE+BE)+(AF-DF)=AE+AF=2AE,则可证得AB+AD=2AE=
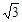
AC


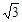 AC,理由见解析解析:
AC,理由见解析解析: ∵∠B和∠D互为补角,
∵∠B和∠D互为补角,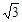 AC. ………………………………………………7分
AC. ………………………………………………7分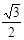 AC.
AC.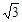 AC. ………………………………………………10分
AC. ………………………………………………10分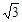 AC
AC