еҰӮеӣҫ3-3-8жүҖзӨәпјҢиҙЁйҮҸдёәmзҡ„ж»‘еқ—жІҝеҖҫи§’дёәОёзҡ„ж–ңйқўдёӢж»‘пјҢж»‘еқ—дёҺж–ңйқўй—ҙзҡ„еҠЁж‘©ж“Ұеӣ ж•°дёәОј,жұӮж»‘еқ—дёӢж»‘зҡ„еҠ йҖҹеәҰ.
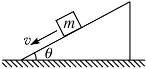
еӣҫ3-3-8
еҰӮеӣҫ3-3-8жүҖзӨәпјҢиҙЁйҮҸдёәmзҡ„ж»‘еқ—жІҝеҖҫи§’дёәОёзҡ„ж–ңйқўдёӢж»‘пјҢж»‘еқ—дёҺж–ңйқўй—ҙзҡ„еҠЁж‘©ж“Ұеӣ ж•°дёәОј,жұӮж»‘еқ—дёӢж»‘зҡ„еҠ йҖҹеәҰ.

еӣҫ3-3-8
ж»‘еқ—жІҝж–ңйқўдёӢж»‘зҡ„еҠ йҖҹеәҰдёә
a=gпјҲsinОё-ОјcosОёпјү
ж–№еҗ‘жІҝж–ңйқўеҗ‘дёӢ.
д»Ҙж»‘еқ—дёәз ”з©¶еҜ№иұЎпјҢиҝӣиЎҢеҸ—еҠӣеҲҶжһҗпјҢж»‘еқ—еҸ—йҮҚеҠӣmgгҖҒж–ңйқўж”ҜжҢҒеҠӣFNе’Ңж»‘еҠЁж‘©ж“ҰеҠӣfдёүеҠӣдҪңз”ЁпјҢеҰӮеҸіеӣҫжүҖзӨәпјҢе»әз«ӢеҰӮеӣҫзӣҙи§’еқҗж Үзі»пјҲе№іиЎҢж–ңйқўеҗ‘дёӢзҡ„ж–№еҗ‘дёәxиҪҙжӯЈж–№еҗ‘пјҢеһӮзӣҙж–ңйқўеҗ‘дёҠзҡ„ж–№еҗ‘дёәyиҪҙжӯЈж–№еҗ‘пјү.
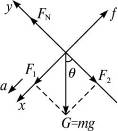
е°ҶйҮҚеҠӣmgжІҝдёӨеқҗж ҮиҪҙжӯЈдәӨеҲҶи§ЈдёәF1=mgsinОё,
F2=mgcosОё
ж №жҚ®зүӣйЎҝ第дәҢе®ҡеҫӢжңүFx=F1-f=ma
Fy=FN-F2=0
з”ұж‘©ж“Ұе®ҡеҫӢжңүf=ОјFN
д»ҘдёҠеҮ ејҸиҒ”з«ӢеҸҜеҫ—ж»‘еқ—жІҝж–ңйқўдёӢж»‘зҡ„еҠ йҖҹеәҰдёә
a=gпјҲsinОё-ОјcosОёпјү
ж–№еҗ‘жІҝж–ңйқўеҗ‘дёӢ.