如图1，在四边形
中，
，
，
是
的直径，
平分
．
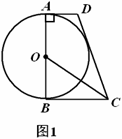
（1）求证：直线
与相切；
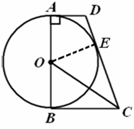
（2）如图2，记（1）中的切点为
，
为优弧
上一点，
，
.求
的值．
如图1，在四边形中，，，是的直径，平分．
（1）求证：直线与相切；
（2）如图2，记（1）中的切点为，为优弧上一点，，.求的值．
（1）证明见解析；（2）
．
【解析】
（1）如图（见解析），先根据平行线的性质得出
，再根据角平分线的性质可得
，然后根据圆的切线的判定即可得证；
（2）如图（见解析），先根据圆周角定理可得
，
，再根据圆的切线的判定、切线长定理可得
，然后根据相似三角形的判定与性质可得
，设
，从而可得
，又根据相似三角形的判定与性质可得
，从而可得
，最后根据正切三角函数的定义即可得．
【详解】
（1）如图，过点
作
于点
∵，
∴
，即
又∵平分，
∴
即OE是的半径
∴直线与相切；
（2）如图，连接
，延长
交
延长线于点
由圆周角定理得：，
是的直径，
，
AD、BC都是的切线
由切线长定理得：
∵
∴
在
和
中，
∴
∴
设
，则
在
和
中，
，即
解得
在
中，
则
．
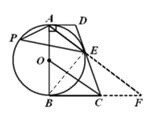
【点睛】
本题考查了圆的切线的判定与性质、圆周角定理、切线长定理、相似三角形的判定与性质、正切三角函数等知识点，较难的是题（2），通过作辅助线，构造相似三角形是解题关键．