设函数f(x)＝
x－lnx(x＞0)，则y＝f(x)( )
(A)在区间(
，1)，(1，e)内均有零点
(B)在区间(，1)，(1，e)内均无零点
(C)在区间(，1)内有零点，在区间(1，e)内无零点
(D)在区间(，1)内无零点，在区间(1，e)内有零点
设函数f(x)＝x－lnx(x＞0)，则y＝f(x)( )
(A)在区间(，1)，(1，e)内均有零点
(B)在区间(，1)，(1，e)内均无零点
(C)在区间(，1)内有零点，在区间(1，e)内无零点
(D)在区间(，1)内无零点，在区间(1，e)内有零点
D.∵f′(x)＝－
，
∴x∈(3，＋∞)时，y＝f(x)单调递增；
x∈(0,3)时，y＝f(x)单调递减.
而0＜＜1＜e＜3，
又f()＝
＋1＞0，f(1)＝＞0，f(e)＝
－1＜0，
∴在区间(，1)内无零点，在区间(1，e)内有零点.
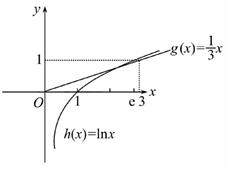
【一题多解】选D.令g(x)＝x，h(x)＝lnx，如图，作出g(x)与h(x)在x>0的图象，可知g(x)与h(x)的图象在(，1)内无交点，在(1，e)内有1个交点，故选D.