设椭圆C:![]() 的离心率e=
的离心率e=![]() ,左顶点M到直线
,左顶点M到直线![]() =1的距离d=
=1的距离d=![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C相交于A,B两点,若以AB为直径的圆经过坐标原点,证明:点O到直线AB的距离为定值;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB的面积S的最小值.
设椭圆C:![]() 的离心率e=
的离心率e=![]() ,左顶点M到直线
,左顶点M到直线![]() =1的距离d=
=1的距离d=![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C相交于A,B两点,若以AB为直径的圆经过坐标原点,证明:点O到直线AB的距离为定值;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB的面积S的最小值.
【解答】解:(Ⅰ)由已知得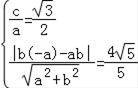 ,又a2=b2+c2,
,又a2=b2+c2,
解得a=2,b=1,c=![]() ,
,
∴椭圆C的方程为![]() .
.
(Ⅱ)证明:设A(x1,y1),B(x2,y2),
①当直线AB的斜率不存在时,则由椭圆的对称性知x1=x2,y1=﹣y2,
∵以AB为直线的圆经过坐标原点,∴![]() =0,
=0,
∴x1x2+y1y2=0,∴![]() ,
,
又点A在椭圆C上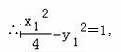 ,
,
解得|x1|=|y1|=![]() .
.
此时点O到直线AB的距离![]() .
.
(2)当直线AB的斜率存在时,设AB的方程为y=kx+m,
联立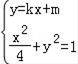 ,得(1+4k2)x2+8kmx+4m2﹣4=0,
,得(1+4k2)x2+8kmx+4m2﹣4=0,
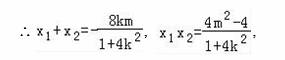
∵以AB为直径的圆过坐标原点O,∴OA⊥OB,
∴![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
∴(1+k2)x1x2+km(x1+x2)+m2=0,
∴(1+k2)•![]() ,
,
整理,得5m2=4(k2+1),
∴点O到直线AB的距离![]() =
=![]() ,
,
综上所述,点O到直线AB的距离为定值![]() .
.
(3)设直线OA的斜率为k0,
当k0≠0时,OA的方程为y=k0x,OB的方程为y=﹣![]() ,
,
联立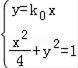 ,得
,得 ,同理,得
,同理,得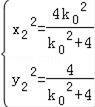 ,
,
∴△AOB的面积S=![]()
![]() =2
=2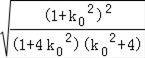 ,
,
令1+![]() =t,t>1,
=t,t>1,
则S=2![]() =2
=2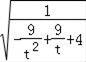 ,
,
令g(t)=﹣![]() +
+![]() +4=﹣9(
+4=﹣9(![]() )2+
)2+![]() ,(t>1)
,(t>1)
∴4<g(t)![]() ,∴
,∴![]() ,
,
当k0=0时,解得S=1,
![]()