已知点M是椭圆C： =1（a＞b＞0）上一点，F1、F2分别为C的左、右焦点

已知点M是椭圆C： =1（a＞b＞0）上一点，F₁、F₂分别为C的左、右焦点，|F₁F₂|=4，∠F₁MF₂=60°，△F₁MF₂的面积为

（Ⅰ）求椭圆C的方程；

（Ⅱ）设N（0，2），过点p（﹣1，﹣2）作直线l，交椭圆C异于N的A、B两点，直线NA、NB的斜率分别为k₁、k₂，证明：k₁+k₂为定值．

【考点】KH：直线与圆锥曲线的综合问题；K3：椭圆的标准方程．

【分析】（I）由余弦定理可得=|MF₁|²+|MF₂|²﹣2|MF₁||MF₂|cos60°，结合|F₁F₂|=2c=4，|MF₁|+|MF₂|=2a，求出a²，b²的值，可得椭圆C的方程；

（Ⅱ）当直线l的斜率存在时，设其方程为y+2=k（x+1），与出椭圆方程联立后，利用韦达定理，化简k₁+k₂可得定值；当直线l斜率不存在时，求出A，B两点坐标，进而求出k₁、k₂，综合讨论结果，可得结论．

【解答】解：（I）在△F₁MF₂中，由|MF₁||MF₂|sin60°=，得|MF₁||MF₂|=．

由余弦定理，得=|MF₁|²+|MF₂|²﹣2|MF₁||MF₂|cos60°=（|MF₁|+|MF₂|）²﹣2|MF₁||MF₂|（1+cos60°）

又∵|F₁F₂|=2c=4，|MF₁|+|MF₂|=2a

故16=4a²﹣16，

解得a²=8，故b²=a²﹣c²=4

故椭圆C的方程为

（Ⅱ）当直线l的斜率存在时，设其方程为y+2=k（x+1）

由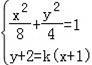，得（1+2k²）x²+4k（k﹣2）x+2k²﹣8k=0

设A（x₁，y₁），B（x₂，y₂），

则x₁+x₂=，x₁x₂=，

从而k₁+k₂=+==2k﹣（k﹣4）=4．                                                  11分

当直线l斜率不存在时，得A（﹣1，），B（﹣1，﹣）

此时k₁+k₂=4

综上，恒有k₁+k₂=4．