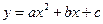 与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程
与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程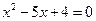 的两个根,且抛物线的对称轴是直线
的两个根,且抛物线的对称轴是直线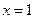 .
.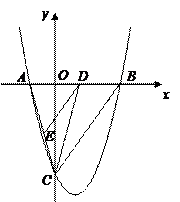
(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?若存在,求出最大值并求此时D点坐标;若不存在,请说明理由.
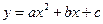 与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程
与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程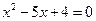 的两个根,且抛物线的对称轴是直线
的两个根,且抛物线的对称轴是直线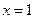 .
.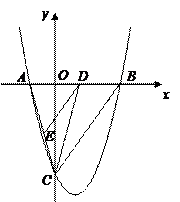
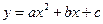 的对称轴为
的对称轴为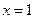
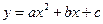 图象上
图象上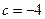
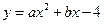 得
得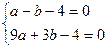 解之得
解之得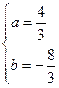

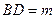 ,则
,则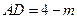
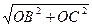 =5
=5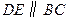 ,∴△ADE∽△ABC
,∴△ADE∽△ABC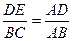
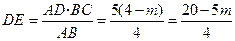
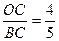
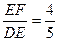
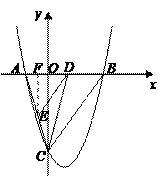 ∴EF=
∴EF=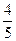 DE=
DE=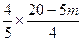 =4-m
=4-m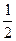 (4-m)×4
(4-m)×4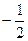 (4-m)( 4-m)
(4-m)( 4-m)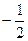 m2+2m(0<m<4)
m2+2m(0<m<4)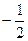 (m-2)2+2, a=
(m-2)2+2, a=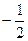 <0
<0