已知抛物线C1:y=﹣![]()
![]() x2﹣(a+1)x﹣a2﹣4a﹣1交x轴于A、B两点(点A在点B的左边),顶点为C.
x2﹣(a+1)x﹣a2﹣4a﹣1交x轴于A、B两点(点A在点B的左边),顶点为C.
(1)求证:不论a为何实数值,顶点C总在同一条直线上;
(2)若∠ACB=90°,求此时抛物线C1的解析式;
(3)在(2)的条件下,将抛物线C1沿y轴负方向平移2个单位得到抛物线C2,直线y=kx﹣2k+1交抛物线C2于E、F两点(点E在点F的左边),交抛物线C2的对称轴于点N,M(xE,3),若MN=ME,求![]()
![]() 的值.
的值.


已知抛物线C1:y=﹣![]()
![]() x2﹣(a+1)x﹣a2﹣4a﹣1交x轴于A、B两点(点A在点B的左边),顶点为C.
x2﹣(a+1)x﹣a2﹣4a﹣1交x轴于A、B两点(点A在点B的左边),顶点为C.
(1)求证:不论a为何实数值,顶点C总在同一条直线上;
(2)若∠ACB=90°,求此时抛物线C1的解析式;
(3)在(2)的条件下,将抛物线C1沿y轴负方向平移2个单位得到抛物线C2,直线y=kx﹣2k+1交抛物线C2于E、F两点(点E在点F的左边),交抛物线C2的对称轴于点N,M(xE,3),若MN=ME,求![]()
![]() 的值.
的值.


【考点】二次函数综合题.
【分析】(1)利用配方法确定顶点坐标,取a=0或﹣1得到两个点,求出经过这两个点的直线的解析式,证明顶点在这条直线上即可.
(2)根据题意写出点B坐标,利用待定系数法即可解决问题.
(3)思想确定点N坐标,作FP⊥对称轴于P,EQ⊥对称轴于Q,设M(m,3),则E(m,﹣![]()
![]() m2+m+1),列出方程求出m的值,再求出E、F两点坐标即可解决问题.
m2+m+1),列出方程求出m的值,再求出E、F两点坐标即可解决问题.
【解答】(1)证明:配方得y=﹣![]()
![]() (x+2+2a)2﹣2a,
(x+2+2a)2﹣2a,
∴顶点C坐标为(﹣2﹣2a,﹣2a),
当a=0时,顶点为(﹣2,0),当a=﹣1时,顶点为(0,2),
设经过(﹣2,0),(0,2)两点的直线为y=kx+b,
则![]()
![]() 解得
解得![]()
![]() ,
,
∴直线解析式为y=x+2,
∵x=﹣2﹣2a时,y=﹣2a,
∴不论a为何实数值,顶点C总在直线y=x+2上.
(2)解:由题意B(﹣2﹣4a,0)代入y=﹣![]()
![]() x2﹣(a+1)x﹣a2﹣4a﹣1,
x2﹣(a+1)x﹣a2﹣4a﹣1,
得到,0=﹣![]()
![]() (﹣2﹣4a)2﹣(a+1)(﹣2﹣4a)﹣a2﹣4a﹣1,
(﹣2﹣4a)2﹣(a+1)(﹣2﹣4a)﹣a2﹣4a﹣1,
整理得,a2+2a=0,
解得a=﹣2或0,
a=0时,抛物线为y=﹣![]()
![]() x2﹣x﹣1,与x轴只有一个交点,不合题意舍弃.
x2﹣x﹣1,与x轴只有一个交点,不合题意舍弃.
∴a=﹣2,此时抛物线解析式为y=﹣![]()
![]() x2+x+3.
x2+x+3.
(3)解:由题意抛物线C2:y=﹣![]()
![]() x2+x+1=﹣
x2+x+1=﹣![]()
![]() (x﹣2)2+2,
(x﹣2)2+2,
∴顶点为(2,2),
∵直线y=kx﹣2k+1,经过定点(2,1),
点(2,1)在对称轴上,
∴点N坐标为(2,1),
作FP⊥对称轴于P,EQ⊥对称轴于Q,设M(m,3),则E(m,﹣![]()
![]() m2+m+1),
m2+m+1),
∵MN=ME,
∴3﹣(﹣![]()
![]() m2+m+1)=
m2+m+1)=![]()
![]() ,
,
解得m=2﹣2![]()
![]() (不符合题意的根已经舍弃),
(不符合题意的根已经舍弃),
∴点E(2﹣2![]()
![]() ,﹣1)代入y=kx﹣2k+1得到k=
,﹣1)代入y=kx﹣2k+1得到k=![]()
![]() ,
,
∴直线解析式为y=![]()
![]() x﹣
x﹣![]()
![]() +1,
+1,
由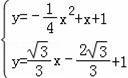
 解得
解得![]()
![]() 或
或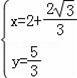
 ,
,
∴点F(2+![]()
![]() ,
,![]()
![]() ),
),
∴EQ=2![]()
![]() ,PF=
,PF=![]()
![]() ,
,
∵EQ∥PF,
∴![]()
![]() =
=![]()
![]() ,
,
∴![]()
![]() =
=![]()
![]() =
=![]()
![]() .
.
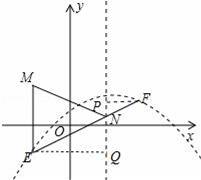

【点评】本题考查二次函数综合题、一次函数、待定系数法等知识,解题的关键是灵活运用待定系数法确定函数解析式,学会用方程的思想思考问题,属于中考压轴题.