不等式组
的解集记为D，有下面四个命题：
p1：∀（x，y）∈D，x+2y≥1，p2：∃（x，y）∈D，x+2y≥2，
p3：∃（x，y）∈D，x+2y≤3，p4：∃（x，y）∈D，x+2y≤﹣1．
其中的真命题是( )
A．p2，p3 B．p1，p2 C．p1，p4 D．p1，p3
不等式组的解集记为D，有下面四个命题：
p1：∀（x，y）∈D，x+2y≥1，p2：∃（x，y）∈D，x+2y≥2，
p3：∃（x，y）∈D，x+2y≤3，p4：∃（x，y）∈D，x+2y≤﹣1．
其中的真命题是( )
A．p2，p3 B．p1，p2 C．p1，p4 D．p1，p3
A
考点：命题的真假判断与应用．
专题：不等式的解法及应用．
分析：作出不等式组 的表示的区域D，对四个选项逐一分析即可．
解答： 解：作出不等式组表示的区域：
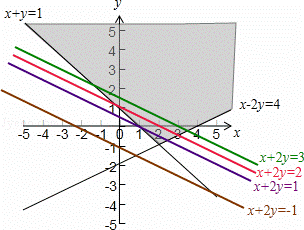
由图知，区域D为直线x+y=1与x﹣2y=4相交的上部角型区域，
显然，区域D有一部分在x+2y=1的下方，故p1：∀（x，y）∈D，x+2y≥1错误；
区域D有一部分在x+2y=2的上方，故p2：∃（x，y）∈D，x+2y≥2正确，
区域D有一部分在x+2y=3的下方，故p3：∃（x，y）∈D，x+2y≤3正确，
区域D全部在x+2y=﹣1的上方，故p4：∃（x，y）∈D，x+2y≤﹣1错误．
综上所述p2，p3正确，
故选：A
点评：本题考查命题的真假判断与应用，着重考查作图能力，熟练作图，正确分析是关键，属于难题．