(11分)已知:在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x
(11分)已知:在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数
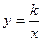
(k>0)的图象与AC边交于点E.
(1)求证:△AOE与△BOF的面积相等.
(2)记S=S
△OEF-S
△ECF,求当k为何值时,S有最大值,最大值为多少?
(3)请探索:是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存
在,请直接写出点F的坐标,若不存在,请说明理由.


(1)证明:设E(x
1,y
1),F(x
2,y
2),△AOE和△FOB的面积分别为S
1、S
2,
由题意得
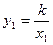
,
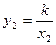
∴
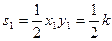
,

∴S
1=S
2 ,即△AOE和△FOB的面积相等.……………………3分
(2)由题意知:E、F两点坐标分别为E(
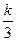
,3)、F(4,
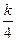
)


S
△ECF=

EC·CF=

(4-
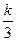
)(3-
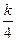
)
S
△EDF=S
矩形AOBC-S
△AOE-S
△ECF=12-

k-

k-S
△ECFS=S
△OEF-S
△ECF=12-k-2 S
△ECF=12-k-2×

(4-
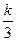
)(3-
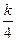
)
S=
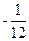
k
2+k,
当k=6时,S有最大值3.…………………7分
(3)存在符合条件的点F,它的坐标为(4,
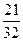
)……………………11分解析:
略
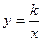 (k>0)的图象与AC边交于点E.
(k>0)的图象与AC边交于点E.

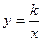 (k>0)的图象与AC边交于点E.
(k>0)的图象与AC边交于点E.

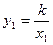 ,
,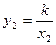
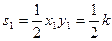 ,
, 
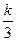 ,3)、F(4,
,3)、F(4,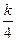 )
)

 EC·CF=
EC·CF= (4-
(4-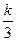 )(3-
)(3-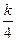 )
) k-
k- k-S△ECF
k-S△ECF (4-
(4-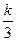 )(3-
)(3-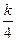 )
)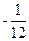 k2+k,
k2+k,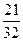 )……………………11分解析:
)……………………11分解析: