已知函数![]() ,.
,.
(Ⅰ)设曲线y= f(x)在点(1, f(1))处的切线为l,若l与圆x2+ (y-1)2=1相切,求k 的值
(2)若![]() ,且对于任意实数
,且对于任意实数![]() 时,
时,![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,求证:
,求证:![]()
已知函数![]() ,.
,.
(Ⅰ)设曲线y= f(x)在点(1, f(1))处的切线为l,若l与圆x2+ (y-1)2=1相切,求k 的值
(2)若![]() ,且对于任意实数
,且对于任意实数![]() 时,
时,![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,求证:
,求证:![]()
解.(1)依题意有,![]() = ex-k. ……(1分)
= ex-k. ……(1分)
因此过![]() 点的直线的斜率为 e - k,又f(1)= e -k
点的直线的斜率为 e - k,又f(1)= e -k
所以,过![]() 点的直线方程为 y –(e -k)= (e -k)(x – 1)
点的直线方程为 y –(e -k)= (e -k)(x – 1)
即.(e -k) x – y = 0 ……………………………………………(2分)
又已知圆的圆心为(0,1),半径为![]() ,依题意,
,依题意,

解得![]() ……………………………………………(4分)
……………………………………………(4分)
(2)法一: 由![]() 得
得![]() .
.
①当![]() 时,
时,![]() .
.
此时![]() 在
在![]() 上单调递增.
上单调递增.
故![]() ,符合题意.……………………………………………(6分)
,符合题意.……………………………………………(6分)
②当![]() 时,
时,![]() .
.
当![]() 变化时
变化时![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由此可得,在![]() 上,
上,![]() .
.
依题意,![]() ,又
,又![]() .
.
综合①,②得,实数![]() 的取值范围是
的取值范围是![]() .……………………………………(9分)
.……………………………………(9分)
法二:(分离参数法)![]() >0 , 在x≥0恒成立
>0 , 在x≥0恒成立
若 X=0时 ,k为任意实数……………………………………………(6分)
若 X﹥0时 ,![]() >0在x>0恒成立
>0在x>0恒成立
即k<ex/x在x>0恒成立, 再利导数法求出Q(x)=ex/x在x>0上的最小值
Q(x)min= Q(1)=e ∴0<k<e
实数![]() 的取值范围是
的取值范围是![]() ……………………………………………(9分)
……………………………………………(9分)
(3)![]() ,
,
![]()
![]() ,…(11分)
,…(11分)
![]() ,
,
![]()
![]()
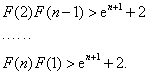
由此得,![]()
![]()
故![]() .……………………………………(13分)
.……………………………………(13分)