中，
，
.沿它的对角线
把△
折起，使点
到达平面
外点
的位置.
（Ⅰ）证明：平面
平面
；
（Ⅱ）如果△
为等腰三角形，求二面角
的大小.
中，，.沿它的对角线把△折起，使点到达平面外点的位置.
（Ⅰ）证明：平面平面；
（Ⅱ）如果△为等腰三角形，求二面角的大小.
，，所以，. 因为折叠过程中，，所以，又，
故平面.
又平面
，所以平面
平面
.
（Ⅱ）解法一：如图，延长
到
，使
，连结
，
.
因为
，
，
，
，所以
为正方形，
.
由于
，
都与平面
垂直，所以
，可知
.
因此只有
时，△
为等腰三角形.
在
△
中，
，又
，所以△
为等边三角形，
.
由（Ⅰ）可知，
，所以
为二面角
的平面角，即二面角
的大小为
.
解法二：以
为坐标原点，射线
，
分别为
轴正半轴和
轴正半轴，建立如图的空间直角坐标系
，则
，
，
.
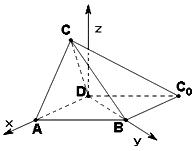
由（Ⅰ）可设点
的坐标为
，其中
，则有
. ①
因为△
为等腰三角形，所以
或
.
若
，则有
.
则此得
，
，不合题意.
若
，则有
. ②
联立①和②得
，
. 故点
的坐标为
.
由于
，
，所以
与
夹角的大小等于二面角
的大小.
又
，
，
所以
即二面角
的大小为
.