水平冰面上两个质量均为m的滑冰者A和B，分别以大小为vA和vB的水平速度相向运动(如图所示)。当它们趋近到一定距离时，为避免相撞，A立即沿水平方向向B扔出一个动量大小为p(相对地面，下同)、质量可以忽略的沙包，沙包在B手中停留一段时间T后又以大小相同的动量p水平扔回A手中，A又经相同时间T再次以同样大小的动量水平扔给B，并不断重复上述过程，最终两个滑冰者避免了相撞。设水平冰面摩擦不计，除沙包在A、B手中停留的时间T外，不计空中飞行的时间。求：
(1)滑冰者B第一次把沙包接到手中时A、B的速度；
(2)从A开始扔沙包算起，沙包在A、B之间至少被扔出几次才可以避免两个滑冰者相撞?
解：(1)取水平向左为正方向，第一次A扔沙包、B接沙包，设A扔沙包后速度为
，对A扔沙包，由动量守恒定律有：mvA=m
+p ① 对B接沙包，由动量守恒定律有：-mvB=m
由①②可得：
③ 
④ (2)第二次是B扔沙包、A接沙包，设B扔沙包后速度为
，对B扔沙包，由动量守恒定律有：m
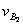
-P ⑤ 对A接沙包，由动量守恒定律有：m
⑥ 由③-⑥可得：
⑦ 
⑧ 设n次扔沙包、接沙包后A的速度为vAn，B的速度为vBn，则由上述推理可得
vAn=vA-n
⑩ 要使A、B不相撞且扔沙包次数最少，应满足
因此，满足A、B不相撞所需的最少扔沙包次数n=
所以，当
次 当
+1]次