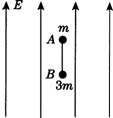
(1)电场强度及细绳断开后A、B两球的加速度.
(2)当B球速度为零时,A球速度的大小.
(3)从绳断开至B球速度为零的过程中,两球组成系统的机械能增量为多少?

(1)电场强度及细绳断开后A、B两球的加速度.
(2)当B球速度为零时,A球速度的大小.
(3)从绳断开至B球速度为零的过程中,两球组成系统的机械能增量为多少?
解:(1)由于两小球是匀速上升的,由平衡条件有2qE=4mg
解得电场强度E=![]() .
.
绳断开后,对A球由牛顿第二定律有qE-mg=maA
解得aA=g,方向向上.
对B球有qE-3mg=3maB
解得aB=-![]() g,方向向下.
g,方向向下.
(2)两球所组成系统的动量守恒,当B球的速度为零时,有(m+
解得vA=4v0.
(3)绳断开后,B球匀减速上升,设当速度为零时所用的时间为t,则t=![]() =
=![]()
此过程A、B球上升的高度分别为
hA=![]()
hB=![]() =
=![]()
此过程中,两球所组成系统的机械能的增量等于电场力对两球做的功,即ΔE=qEhA+qEhB=18
m![]()