定义：如图1，抛物线y=ax2+bx+c（a≠0）与x轴交于A，B两点，点P在该抛物线上（P点与A、B两点不重合），如果△ABP的三边满足AP2+BP2=AB2，则称点P为抛物线y=ax2+bx+c（a≠0）的勾股点.
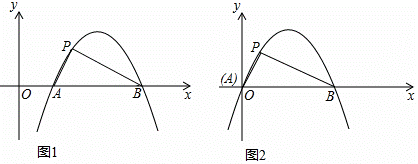
(1)直接写出抛物线y=﹣x2+1的勾股点的坐标.
(2)如图2，已知抛物线C：y=ax2+bx（a≠0）与x轴交于A，B两点，点P（1，
）是抛物线C的勾股点，求抛物线C的函数表达式.
(3)在(2)的条件下，点Q在抛物线C上，求满足条件S△ABQ=S△ABP的Q点（异于点P）的坐标.
解：(1)抛物线y=﹣x2+1的勾股点的坐标为（0，1）；
(2)抛物线y=ax2+bx过原点，即点A（0，0），
如图，作PG⊥x轴于点G，
∵点P的坐标为（1，
），
∴AG=1、PG=，PA=
=
=2，
∵tan∠PAB=
=，
∴∠PAG=60°，
在Rt△PAB中，AB=
=
=4，
∴点B坐标为（4，0），
设y=ax（x﹣4），
将点P（1，
）代入得：a=﹣
，
∴y=﹣
x（x﹣4）=﹣x2+
x；
(3)①当点Q在x轴上方时，由S△ABQ=S△ABP知点Q的纵坐标为
，
则有﹣
x2+
x=
，
解得：x1=3，x2=1（不符合题意，舍去），
∴点Q的坐标为（3，）；
②当点Q在x轴下方时，由S△ABQ=S△ABP知点Q的纵坐标为﹣，
则有﹣x2+x=﹣
，
解得：x1=2+
，x2=2﹣，
∴点Q的坐标为（2+，﹣）或（2﹣，﹣）；
综上，满足条件的点Q有3个：（3，）或（2+
，﹣
）或（2﹣，﹣）．