如图，在平面直角坐标系xOy中，抛物线L1：y＝x2+bx+c过点C（0，﹣3）

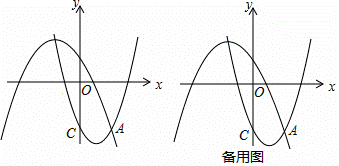
如图，在平面直角坐标系xOy中，抛物线L₁：y＝x²+bx+c过点C（0，﹣3），与抛物线L₂：y＝﹣x²﹣x+2的一个交点为A，且点A的横坐标为2，点P、Q分别是抛物线L₁、L₂上的动点．

（1）求抛物线L₁对应的函数表达式；

（2）若以点A、C、P、Q为顶点的四边形恰为平行四边形，求出点P的坐标；

（3）设点R为抛物线L₁上另一个动点，且CA平分∠PCR．若OQ∥PR，求出点Q的坐标．

【解答】解：（1）将x＝2代入y＝﹣x²﹣x+2，得y＝﹣3，故点A的坐标为（2，﹣3），

将A（2，﹣1），C（0，﹣3）代入y＝x²+bx+c，得

，解得，

∴抛物线L₁：y＝x²﹣2x﹣3；

（2）设点P的坐标为（x，x²﹣2x﹣3），

第一种情况：AC为平行四边形的一条边，

①当点Q在点P右侧时，则点Q的坐标为（x+2，﹣2x﹣3），

将Q（x+2，﹣2x﹣3）代入y＝﹣x²﹣x+2，得

﹣2x﹣3＝﹣（x+2）²﹣（x+2）+2，

解得，x＝0或x＝﹣1，

因为x＝0时，点P与C重合，不符合题意，所以舍去，

此时点P的坐标为（﹣1，0）；

②当点Q在点P左侧时，则点Q的坐标为（x﹣2，x²﹣2x﹣3），

将Q（x﹣2，x²﹣2x﹣3）代入y＝﹣x²﹣x+2，得

y＝﹣x²﹣x+2，得

x²﹣2x﹣3＝﹣（x﹣2）²﹣（x﹣2）+2，

解得，x＝3，或x＝﹣，

此时点P的坐标为（3，0）或（﹣，）；

第二种情况：当AC为平行四边形的一条对角线时，

由AC的中点坐标为（1，﹣3），得PQ的中点坐标为（1，﹣3），

故点Q的坐标为（2﹣x，﹣x²+2x﹣3），

将Q（2﹣x，﹣x²+2x﹣3）代入y＝﹣x²﹣x+2，得

﹣x²+2x﹣3═﹣（2﹣x）²﹣（2﹣x）+2，

解得，x＝0或x＝﹣3，

因为x＝0时，点P与点C重合，不符合题意，所以舍去，

此时点P的坐标为（﹣3，12），

综上所述，点P的坐标为（﹣1，0）或（3，0）或（﹣，）或（﹣3，12）；

（3）当点P在y轴左侧时，抛物线L₁不存在点R使得CA平分∠PCR，

当点P在y轴右侧时，不妨设点P在CA的上方，点R在CA的下方，

过点P、R分别作y轴的垂线，垂足分别为S、T，

过点P作PH⊥TR于点H，则有∠PSC＝∠RTC＝90°，

由CA平分∠PCR，得∠PCA＝∠RCA，则∠PCS＝∠RCT，

∴△PSC∽△RTC，

∴，

设点P坐标为（x₁，），点R坐标为（x₂，），

所以有，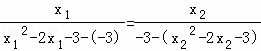

整理得，x₁+x₂＝4，

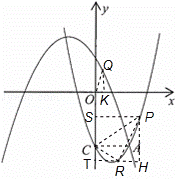
在Rt△PRH中，tan∠PRH＝＝

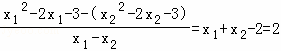
过点Q作QK⊥x轴于点K，设点Q坐标为（m，），

若OQ∥PR，则需∠QOK＝∠PRH，

所以tan∠QOK＝tan∠PRH＝2，

所以2m＝，

解得，m＝，

所以点Q坐标为（，﹣7+）或（，﹣7﹣）．