,PC＝1,求PD的长.
图2-5-15
,PC＝1,求PD的长.
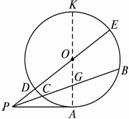
图2-5-15
思路分析
:求PD,可使用割线定理PC·PB＝PD·PE,显然PA切⊙O,∴PA2＝PC·PB.可求得PB,但PE ＝PD +DE,DE为⊙O直径,所以求⊙O的直径成为解题的关键.
解
:∵PA切⊙O于A,∴PA2＝PC·PB.
又PB＝PC+BC,
∴BC＝11.
连结AO,并延长与⊙O交于K,与CB交于G,
则GA＝PA tan∠GPA＝PA tan30°＝2.
又Rt△GPA中,∠GPA＝30°,
∴PG ＝2GA ＝4.∴CG ＝3,GB ＝8.
由相交弦定理GC·GB ＝AG·GK,可得GK＝12,
∴直径为14.
∴由割线定理有PC·PB＝PD·PE,得PD ＝-7.