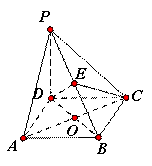
如图,在四棱锥![]() 中,
中,![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,且
,且![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证:![]() ;
;
 (2)已知二面角
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
如图,在四棱锥![]() 中,
中,![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,且
,且![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证:![]() ;
;
 (2)已知二面角
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解:(1)因为![]() 平面
平面![]() ,所以
,所以![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() 又
又![]() 因为
因为![]() 5分
5分
(2)连接![]() 在
在![]() 中,
中,![]() 所以
所以![]() 分别以
分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设![]() 则
则![]() ,
,![]() ,由(1)知,平面
,由(1)知,平面![]() 的一个法向量为
的一个法向量为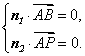 得
得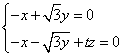 ,令
,令![]() ,得
,得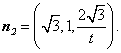 ……8分
……8分
因为二面角![]() 的余弦值为
的余弦值为![]() ,所以
,所以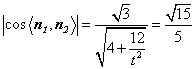 ,
,
解得![]() 或
或![]() (舍去),所以
(舍去),所以![]() …………10分
…………10分
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .因为
.因为![]() ,
,![]() ,所以
,所以![]() 所以
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .12分
.12分