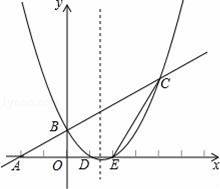
如图，已知一次函数y=的图象与x轴交于A点，与y轴交于B点：抛物线y=

如图，已知一次函数y=的图象与x轴交于A点，与y轴交于B点：抛物线y=的图象余一次函数y=的图象交于B、C两点，与x轴交于D、E两点，且点D的坐标为（1，0）．

（1）求点B的坐标；

（2）求该抛物线的解析式；

（3）求四边形BDEC的面积S；

（4）在x轴上是否存在点P，使得以点P、B、C为顶点的三角形是直角三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．

【考点】二次函数综合题．

【分析】（1）在一次函数y=中，令x=0，即可求出点B的坐标；

（2）将点B、D的坐标代入二次函数解析式，求出b、c的值，即可求出二次函数的解析式；

（3）两解析式联立方程求得B、C的坐标，令y=x²﹣x+1=0，求得D、E的坐标，然后根据梯形和三角形的面积公式求得即可；

（4）设P（x，0），求得PB²=x²+1，PC²=（x﹣4）²+9，BC²=4²+（3﹣1）²=20，然后分三种情况分别讨论求得即可．

【解答】解：（1）∵一次函数y=与y轴的交点为B，

令x=0，可得y=1，

∴B（0，1）；

（2）将B（0，1），D（1，0）的坐标代入y=x²+bx+c得，

，

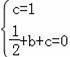
解得：，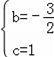

∴解析式为：y=x²﹣x+1；

（3）∵二次函数的图象与一次函数的图象交于B、C两点，

∴，

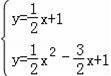
解得：，，

∴C（4，3），

解x²﹣x+1=0，得x=1和x=2，

∴D（1，0），E（2，0），

∴S=（1+3）×4﹣×1×1﹣（4﹣2）×3=4.5；

（4）设P（x，0），

∵B（0，1），C（4，3），

∴PB²=x²+1，PC²=（x﹣4）²+9，BC²=4²+（3﹣1）²=20，

①当∠PBC=90°时，则PB²+BC²=PC²，

即x²+1+20=（x﹣4）²+9，

解得x=，

∴P₁（，0）；

②当∠PCB=90°时，则PC²+BC²=PB²，

即x²+1=（x﹣4）²+9+20，

解得x=，

∴P₂（，0）；

③当∠BPC=90°时，则PB²+PC²=BC²，

即x²+1+（x﹣4）²+9=20，

解得x=1或x=3，

∴P₃（1，0），P₄（3，0）；

∴在x轴上存在点P，使得以点P、B、C为顶点的三角形是直角三角形，点P的坐标为（，0）或（，0）或（1，0）或（3，0）．

【点评】本题是二次函数的综合题，涉及了利用待定系数法求二次函数的解析式、函数图象交点坐标、四边形的面积以及勾股定理的应用等知识，难度适中．