已知实数x，y满足
z=x+ay（a＞1）的最大值为3，则实数a= ．
已知实数x，y满足z=x+ay（a＞1）的最大值为3，则实数a= ．
2 ．
【考点】简单线性规划．
【分析】画出满足条件的平面区域，求出角点的坐标，从而求出z=a+1=3，解出即可．
【解答】解：画出满足条件的平面区域，如图示：
，
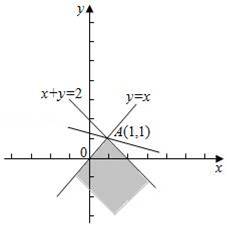由
，解得A（1，1），
∵a＞1，∴﹣1＜﹣
＜0，
∴z=x+ay看化为：y=﹣x+
，
结合图象直线过A（1，1）时，z最大，
z的最大值是z=a+1=3，解得：a=2，
故答案为：2．