在平面直角坐标系
中，点
在椭圆
上，过点
的直线
的方程为
．
（Ⅰ）求椭圆
的离心率；
（Ⅱ）若直线与
轴、
轴分别相交于
两点，试求
面积的最小值；
（Ⅲ）设椭圆的左、右焦点分别为
，
，点
与点关于直线对称，求证：点
三点共线．
在平面直角坐标系中，点在椭圆上，过点的直线的方程为．
（Ⅰ）求椭圆的离心率；
（Ⅱ）若直线与轴、轴分别相交于两点，试求面积的最小值；
（Ⅲ）设椭圆的左、右焦点分别为，，点与点关于直线对称，求证：点
三点共线．
解：（Ⅰ）依题意可知
，
，
所以椭圆离心率为
． …………… 3分
（Ⅱ）因为直线与轴，轴分别相交于两点，所以
．
令
，由得
，则
．
令
，由得
，则
．
所以的面积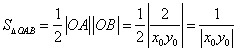
．
因为点
在椭圆上，所以
．
所以
．即
，则
．
所以
．
当且仅当
，即
时，面积的最小值为
． … 9分
（Ⅲ）①当
时，
．
当直线
时，易得
，此时
，
．
因为
，所以三点共线．
同理，当直线
时，三点共线．
②当
时，设点
，因为点与点关于直线对称，
所以
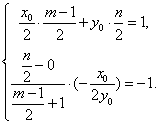整理得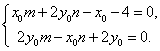
解得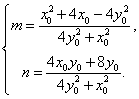
所以点
．
又因为
，
， 且
．
所以
．所以点三点共线．
综上所述，点三点共线． …………………………………14分