泗阳华润苏果超市准备购进A、B两种品牌的书包共100个,已知两种书包的进价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为y元.
| 品牌 | 购买个数(个) | 进价(元/个) | 售价(元/个) | 获利(元) |
| A | x | 50 | 60 | __________ |
| B | __________ | 40 | 55 | __________ |
(1)将表格的信息填写完整;
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
【考点】一次函数的应用.
【分析】(1)设购进A种书包x个,根据超市准备购进A、B两种品牌的书包共100个,可知购进B种书包(100﹣x)个,再根据利润等于每个书包的利润×个数,计算即可求解;
(2)设购进A种书包x个,则购进B种书包(100﹣x)个,根据总利润y=A种书包的利润+B种书包的利润,化简就可以得出结论;
(3)根据购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,列出不等式组求出其解,根据根据一次函数的性质得出答案即可.
【解答】解:(1)填表如下:
| 品牌 | 购买个数(个) | 进价(元/个) | 售价(元/个) | 获利(元) |
| A | x | 50 | 60 | 10x |
| B | 100﹣x | 40 | 55 | 15(100﹣x) |
故答案为100﹣x;10x;15(100﹣x);
(2)y=10x+15(100﹣x)=﹣5x+1500,
即y关于x的函数表达式为y=﹣5x+1500;
(3)由题意可得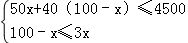 ,
,
解得25≤x≤50,
∵y=﹣5x+1500,﹣5<0,
∴y随x的增大而减小,
∴当x=25时,y有最大值,最大值为:﹣5×25+1500=1375(元).
即当购进A种书包25个,B种书包75个时,超市可以获得最大利润;最大利润是1375元.
【点评】本题考查了一次函数的实际运用,根据利润=售价﹣进价来确定一次函数的解析式,列一元一次不等式组解实际问题,在解答时求出一次函数的解析式是关键.
