设A1、A2是椭圆+=1(a>b>0)长轴的两个端点,P1P2是垂直于x轴的弦,求直

设A₁、A₂是椭圆

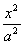
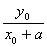
=1(a>b>0)长轴的两个端点,P₁P₂是垂直于x轴的弦,求直线A₁P₁、A₂P₂的交点P的轨迹方程.

答案

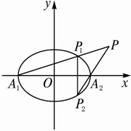
解析

:设A₁(-a,0),A₂(a,0),P₁(x₀,y₀),P₂(x₀,-y₀),

则l_A1P1:y=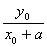

(x+a),l_A2P2:y=

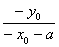
(x-a).

两式相乘得y²=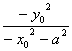

(x²-a²),注意到

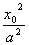
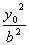
=1,

∴直线A₁P₁、A₂P₂交点P的轨迹方程是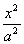

=1(y≠0).

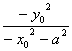
在一定的温度和压强下，气体的体积主要决定于（） A．气体分子粒子大小 B．气体分子数目的多少 C．

免疫球蛋白IgG的结构示意图如图．其中﹣s﹣s表示连接两条相邻肽链的二硫链．若该lgG由m个氨基酸构成，则该lgG有肽键数（） A．

( 8分)一列车从静止开始，以1m/s加速度做匀加速直线运功，20s后以其术速度做匀速直线运动，又经过一段时间后，又以2m/s的加速度做匀减速直线运动，

小明同学用蜡烛、凸透镜和光屏做“探究凸透镜成像规律”的实验．（1）如图所示，要使像能够成在光屏的中央，应将光屏向（选填“上”

Orange can bring you success and ______ when you are feeling sad. A. cheer up you B. cheers up you C. cheer you up D. cheers you up

爱莲说（10分）水陆草木之花，可爱者甚蕃。晋陶渊明独爱菊。自李唐来，世人盛爱牡丹。予独爱莲之出淤泥而不染，濯清涟而不妖，中通外直，不蔓

阅读下面的文字，写一则短评。要求：观点鲜明，见解独到，不少于50字。（4分）这几年，高考加分泛滥，高考的分数，加还是不加，困扰着学生、家

“研表究明，汉字的序顺并不定一能影阅响读，比如当你看完这句话后，才发这现里的字全是乱的。” 之所以产生这种现象，是由人脑的“阅读惯性