如图1-1-10,已知在梯形ABCD中,AD∥BC,∠ADC=90°,E是AB边的中点,连结ED、EC.求证:ED=EC.
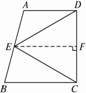
图1-1-10
如图1-1-10,已知在梯形ABCD中,AD∥BC,∠ADC=90°,E是AB边的中点,连结ED、EC.求证:ED=EC.

图1-1-10
思路解析
:在梯形中,若已知一腰的中点,一般过这点作底边的平行线即可得到另一腰的中点.所以由E是AB边的中点,作EF∥BC交DC于F,即可得EF⊥DC,从而利用线段中垂线的性质得到结论.证明
:过E点作EF∥BC交DC于F,∵在梯形ABCD中,AD∥BC,
∴AD∥EF∥BC.
∵E是AB的中点,
∴F是DC的中点(经过梯形一腰中点与底平行的直线必平分另一腰).
∵∠ADC =90°,
∴∠DFE =90°.
∴EF⊥DC于F.
又∵F是DC中点,
∴EF是DC的垂直平分线.
∴ED =EC(线段垂直平分线上的点到线段两端点距离相等).