正三角形
的边长为
，将它沿平行于
的线段
折起（其中
在边
上，
在
边上），使平面
平面
。
，
分别是，的中点.
（1）证明：
平面
；
（2）若折叠后，
，
两点间的距离为
，求最小时，四棱锥
的体积.
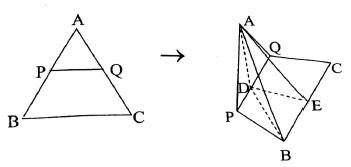
正三角形的边长为，将它沿平行于的线段折起（其中在边上，在边上），使平面平面。，分别是，的中点.
（1）证明：平面；
（2）若折叠后，，两点间的距离为，求最小时，四棱锥的体积.
Ⅰ）证明：连接
，
，
，在
中，
，是的中点，所以
.
又因为是等腰梯形的对称轴，所以
.
而
，所以平面.
（II）解： 因为平面平面，，所以
平面
，连结
，则
.
设
，
（为的中点），
于是
.
因此
，
当
时，
.
此时四棱锥的体积为
.