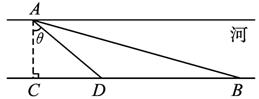
解：如题图所示，AD是水下电缆，DB是地下电缆.作AC⊥BD，AC=1，AB=4，则BC=
，设∠CAD=θ，则θ∈(0，arccos
).∵AD=
=secθ，BD=BC-CD=
-tanθ，依题意，由A、B铺设电缆的总费用为y=4secθ+2（
-tanθ）=
+2
.设μ=
（μ＞0），则2sinθ+μcosθ=4.∴sin（θ+φ）=
φ=arctan
.∵ sin（θ+φ）≤1.∴
≥4，解得μ≥2
.∴ymin=2
+2
.此时φ=arctan
=
，θ=
，BD=
-
.因此，水下电缆应从距B城(
-
)千米处向A城铺设，总施工费用最少.