一质量为M的平板小车，在光滑水平面上以速度v0匀速前进，如果在小

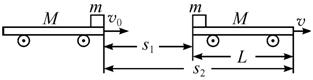
图1

分析与解答：

解法1：取地面为参照系，小木块m做初速度为零的匀加速直线运动，平板车M做初速度为v₀的匀减速直线运动。

对m用牛顿第二定律得：

F_f=μmg=ma₁                                    ①

对M用牛顿第二定律得：

F′_f=Ma₂                                      ②

由牛顿第三定律得：F_f=-F′_f                    ③

设经过t后，小木块恰好滑到小车的后边缘，此时木块与车保持相对静止，对地有共同的速度v,则：

v=a₁t=v₀+a₂t₂                                  ④

所以，小车的最短长度:

L=s₂-s₁

=(v₀t＋

由①—⑤得：

t=

解法2：依题作出图2，设m和M相互作用，经历的时间为t，二者具有共同的速度v，系统在水平方向上不受外力作用动量守恒，则有：

图2

Mv₀=(M+m)v                                ①

对小木块m用动量定理：

μmgt=mv                                 ②

因m和M都作匀变速直线运动，对小木块m有：

s₁=

对小车有：

s₂=

则小车的最短长度为：

L=s₂-s₁=

解法3：由解法2得到M和m的共同速度：

v=

对两者在相互作用的过程用动能定理得：

对m有：

μmgs₁=

对M有：

-μmgs₂=

解①②③式，得到小车的最短的长度：

L=s₂-s₁=

解法4：如选小车为参照系，则小木块m相对于小车M的初速度为-v₀，末速度v′=0,作匀减速运动，相对于小车的加速度：

a_相=a₁-a₂=μg(1+

因此在时间t内，m在M上滑行的距离L=｜

解法5：小木块m和小车M都作匀变速直线运动，依题意可作出它们的v-t图象，如图3所示。根据v-t图象与坐标轴所包围的面积的物理意义可知，ΔOBv₀的面积大小即小车的最短长度，则有：

图3

L=

解法6：(整体法)选取小木块和小车为一系统，两者在相互作用过程中水平方向不受外力作用，动量守恒，则有：

Mv₀=(m+M)v                               ①

系统相互作用过程中，损失的机械能等于系统产生的热量。根据能量守恒定律得：

μmgL=

由①②解得，相对位移L，即小车的最短长度为：

L=