如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为 .
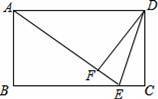

如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为 .


2![]()
![]() .
.
【考点】翻折变换(折叠问题);矩形的性质.
【分析】由翻折易得△DFE≌△DCE,则DF=DC,∠DFE=∠C=90°,再由AD∥BC得∠DAF=∠AEB,根据AAS证出△ABE≌△DFA;则AE=AD,设CE=x,从而表示出BE,AE,再由勾股定理,求得DE.
【解答】证明:由矩形ABCD,得∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,
由AD∥BC得∠DAF=∠AEB,
∴在△ABE与△DFA中,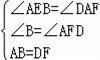
 ,
,
∴△ABE≌△DFA(AAS).
∵由EC:BE=1:4,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=6,
∴x=2,
在Rt△DCE中,DE=![]()
![]() =
=![]()
![]() =2
=2![]()
![]() .
.
故答案是:2![]()
![]() .
.


【点评】本题考查了三角形的全等和勾股定理的应用,一定要熟练掌握全等三角形的判定方法和勾股定理的内容.