①f（
）=1；②函数的值域为[-1,1]；
③严格递减；④f（xy）=f（x）+f（y）.
（1）求证：
不在f（x）的定义域内；
（2）求不等式f-1（x）·f-1（
）≤
的解集.
①f（）=1；②函数的值域为[-1,1]；
③严格递减；④f（xy）=f（x）+f（y）.
（1）求证：不在f（x）的定义域内；
（2）求不等式f-1（x）·f-1（）≤的解集.
（1）证明：假设在f（x）的定义域内，
则f（）=f（×）=f（
）+f（
）=2，
与2
［-1，1］矛盾.
∴
不在定义域内.
（2）解：由f-1（x）·f-1（
）≤
，又严格递减，
∴f［f-1（x）·f-1（
）］≥f（
）.
∴x+
≥1.又考虑到值域为[-1,1]，
∴有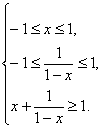
解得x=0.
∴{x|x=0}.