如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°．点E为底AD上一点，将△AB

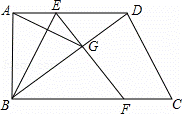
如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°．点E为底AD上一点，将△ABE沿直线BE折叠，点A落在梯形对角线BD上的G处，EG的延长线交直线BC于点F．

（1）点E可以是AD的中点吗？为什么？

（2）求证：△ABG∽△BFE；

（3）设AD=a，AB=b，BC=c

    ①当四边形EFCD为平行四边形时，求a，b，c应满足的关系；

    ②在①的条件下，当b=2时，a的值是唯一的，求∠C的度数．

考点：

相似形综合题；根的判别式；根与系数的关系；平行四边形的性质；直角梯形；翻折变换（折叠问题）；相似三角形的判定与性质。

专题：

代数几何综合题。

分析：

（1）根据折叠的性质可得AE=GE，∠EGB=∠EAB=90°，再根据直角三角形斜边大于直角边可得DE＞EG，从而判断点E不可能是AD的中点；

（2）方法一：根据两直线平行，内错角相等可得∠AEB=∠EBF，再根据折叠的性质可以判定出∠AEB=∠BEG，然后得到∠EBF=∠BEF，从而判断出△FEB为等腰三角形，再根据等角的余角相等求出∠ABG=∠EFB，然后根据等腰三角形的两个底角相等求出∠BAG=∠FBE，然后根据两角对应相等，两三角形相似即可证明；

方法二：与方法一相同求出∠ABG=∠EFB后，根据等腰三角形的两腰相等，然后根据两边对应成比例且夹角相等判断出两个三角形相似；

（3）①方法一：根据勾股定理求出BD的长度，再利用两角对应相等，两三角形相似得到△ABD和△DCB相似，然后根据相似三角形对应边成比例列式计算即可得解；

方法二：过点D作DH⊥BC于点H，然后求出∠C=∠ABD，再根据直角相等，判断出△ABD和△HCD相似，根据相似三角形对应边成比例列式计算即可得解；

方法三：先求出△ABD和△GFB相似，根据相似三角形对应边成比例列式求出BF的长度，再求出△EDG和△FBG相似，根据平行四边形的对边相等表示出ED，再表示出DG，然后根据相似三角形对应边成比例列式整理即可得证；

②方法一：把b=2代入a、b、c的关系式，利用求根公式求出a的两个根，再根据a是唯一的，可以判定△=c²﹣16=0，然后求出c=4，再代入根求出a=2，然后判断出H是BC的中点，利用解直角三角形求出∠C=45°；

方法二：把b=2代入a、b、c的关系式，利用根与系数的关系判断出关于a的方程的解是正数，再根据a是唯一的，可以判定△=c²﹣16=0，然后求出c=4，再代入根与系数的关系求出a=2，然后判断出H是BC的中点，利用解直角三角形求出∠C=45°．

解答：

解：（1）不是．…1分

据题意得：AE=GE，∠EGB=∠EAB=90°，

∴Rt△EGD中，GE＜ED，

∴AE＜ED，

故，点E不可以是AD的中点；…2分

（注：大致说出意思即可；反证法叙述也可）

（2）方法一：

证明：∵AD∥BC，

∴∠AEB=∠EBF，

∵△EAB≌△EGB，

∴∠AEB=∠BEG，

∴∠EBF=∠BEF，

∴FE=FB，

∴△FEB为等腰三角形．

∵∠ABG+∠GBF=90°，∠GBF+∠EFB=90°，

∴∠ABG=∠EFB，…4分

在等腰△ABG和△FEB中，∠BAG=（180°﹣∠ABG）÷2，

∠FBE=（180°﹣∠EFB）÷2，

∴∠BAG=∠FBE，…5分

∴△ABG∽△BFE，（注：证一对角对应等评2分，第二对角对应等评1分，该小问3分，若只证得△FEB为等腰三角形，评1分．）

方法二：∠ABG=∠EFB（见方法一），…4分

证得两边对应成比例：，…5分

由此可得出结论．

（注：两边对应成比例，夹角等证得相似，若只证得△FEB为等腰三角形，评1分．）

（3）①方法一：∵四边形EFCD为平行四边形，

∴EF∥DC，

证明两个角相等，得△ABD∽△DCB，…7分

∴，

即，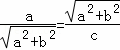

∴a²+b²=ac；…8分

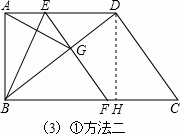
方法二：如图，过点D作DH⊥BC，

∵四边形EFCD为平行四边形

∴EF∥DC，

∴∠C=∠EFB，

∵△ABG∽△BFE，

∴∠EFB=∠GBA，

∴∠C=∠ABG，

∵∠DAB=∠DHC=90°，

∴△ABD∽△HCD，…7分

∴，

∴，

∴a²+b²=ac；…8分（注：或利用tan∠C=tan∠ABD，对应评分）

方法三：证明△ABD∽△GFB，则有，

∴，则有BF=，…6分

∵四边形EFCD为平行四边形，

∴FC=ED=c﹣，

∵ED∥BC，

∴△EDG∽△FBG，

∴，

∴，

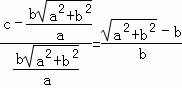∴a²+b²=ac；…8分

②方法一：解关于a的一元二次方程a²﹣ac+2²=0，得：

a₁=，a₂=…9分

由题意，△=0，即c²﹣16=0，

∵c＞0，

∴c=4，

∴a=2…10分

∴H为BC的中点，且ABHD为正方形，DH=HC，∠C=45°；…11分

方法二：设关于a的一元二次方程a²﹣ac+2²=0两根为a₁，a₂，

a₁+a₂=c＞0，a₁•a₂=4＞0，

∴a₁＞0，a₂＞0，…9分

由题意，△=0，即c²﹣16=0，

∵c＞0，

∴c=4，

∴a=2，…10分

∴H为BC的中点，且ABHD为正方形，DH=HC，∠C=45°．…11分

点评：

本题综合考查了相似三角形的性质与判定，根的判别式，根与系数的关系，平行四边形的性质，折叠的性质，综合性较强，难度较大，需仔细分析，认真研究，结合图形理清题目边长之间的关系，角度之间的关系是解题的关键，本题对同学们的能力要求较高．